广东省深圳市龙岗区2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-10-20 类型:期末考试
一、单选题
-
1. -4的绝对值是( )A、4 B、±4 C、-4 D、2. 2019年天猫“双11”总成交额再破纪录约为268400000000元!在24小时的交易中,广东人“剁手”指数最高,再度蝉联第一名.区县方面,深圳龙岗区居全省第三,其中268400000000元用科学记数法表示为( )A、 B、 C、 D、3. 下列各图中,经过折叠能围成一个正方体的是( )A、
 B、
B、 C、
C、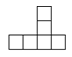 D、
D、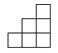 4.
4.如图的几何体的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,下列说法中错误的是( )
5. 如图,下列说法中错误的是( ) A、OA方向是北偏东40° B、OB方向是北偏西15° C、OC方向是南偏西30° D、OD方向是东南方向6. 下列说法正确的是( )A、3a-5的项是3a,5 B、 是二次三项式 C、 与 是同类项式 D、单项式 的系数是-37. 已知 是关于x的方程 的解,则a的值为A、 B、 C、 D、18. “植树时只要定出两棵树的位置,就能确定这一行树所在的直线”,用数学知识解释其道理应是( )A、两点确定一条直线 B、两点之间,线段最短 C、直线可以向两边延长 D、两点之间线段的长度,叫做这两点之间的距离9. 下面调查统计中,适合采用普查方式的是( )A、华为手机的时长占有率 B、乘坐飞机的旅客是否携带了违禁物品 C、某市市民对中美贸易摩擦的知晓情况 D、“比亚迪”汽车每百公里的耗油量10. 扇子是引风用品,夏令营必备之物,纸扇在DE与BC之间糊有纸条,可以题字或者作画.如图,竹条AD的长为5cm,贴纸的部分BD的长为10cm.扇形纸扇完全打开后,外侧两竹条AB,AC夹角为120℃,则纸扇贴纸部分的面积为( )
A、OA方向是北偏东40° B、OB方向是北偏西15° C、OC方向是南偏西30° D、OD方向是东南方向6. 下列说法正确的是( )A、3a-5的项是3a,5 B、 是二次三项式 C、 与 是同类项式 D、单项式 的系数是-37. 已知 是关于x的方程 的解,则a的值为A、 B、 C、 D、18. “植树时只要定出两棵树的位置,就能确定这一行树所在的直线”,用数学知识解释其道理应是( )A、两点确定一条直线 B、两点之间,线段最短 C、直线可以向两边延长 D、两点之间线段的长度,叫做这两点之间的距离9. 下面调查统计中,适合采用普查方式的是( )A、华为手机的时长占有率 B、乘坐飞机的旅客是否携带了违禁物品 C、某市市民对中美贸易摩擦的知晓情况 D、“比亚迪”汽车每百公里的耗油量10. 扇子是引风用品,夏令营必备之物,纸扇在DE与BC之间糊有纸条,可以题字或者作画.如图,竹条AD的长为5cm,贴纸的部分BD的长为10cm.扇形纸扇完全打开后,外侧两竹条AB,AC夹角为120℃,则纸扇贴纸部分的面积为( ) A、 cm2 B、 cm2 C、 cm2 D、100πcm211. 2018年电影《我不是药神》反映了进口药用药贵的事实,从而引起了社会的广泛关注.国家针对部分药品进行改革,看病贵将成为历史.某药厂对售价为m元的药品进行了降价,现在有三种方案.
A、 cm2 B、 cm2 C、 cm2 D、100πcm211. 2018年电影《我不是药神》反映了进口药用药贵的事实,从而引起了社会的广泛关注.国家针对部分药品进行改革,看病贵将成为历史.某药厂对售价为m元的药品进行了降价,现在有三种方案.方案一:第一次降价10%,第二次降价30%;
方案二:第一次降价20%,第二次降价15%;
方案三:第一、二次降价均为20%.三种方案哪种降价最多( )
A、方案一 B、方案二 C、方案三 D、不能确定12. “数形结合”是一种重要的数学思维,观察下面的图形和算式:1=1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9═25=52
解答下列问题:请用上面得到的规律计算:1+3+7+……+101=( )
 A、2601 B、2501 C、2400 D、2419
A、2601 B、2501 C、2400 D、2419二、填空题
-
13. 15度=分14. 小明和小聪坐公交从学校去体育馆参加运动会,他们从学校门口的公交车站上车,上车后发现包括他们俩共13人,经过2个站点小明观察到上下车情况如下(记上车为正,下车为负):A(+4,-2),B(+6,-5).经过A,B这两站点后,车上还有人.15. 如图∠BOC=2∠AOC,OD平分∠AOB,OE平分∠AOC,则∠DOE与∠AOB的数量关系为:.
 16. 如图,已知线段AB,按下列要求自己完成画图并计算,延长线段AB到点C,使BC=2AB,取AC中点D;如果AB=6,则线段BD的长度为.
16. 如图,已知线段AB,按下列要求自己完成画图并计算,延长线段AB到点C,使BC=2AB,取AC中点D;如果AB=6,则线段BD的长度为.
三、解答题
-
17. 计算:(1)、(2)、18. 解方程(1)、(2)、19. 央视举办的《中国诗词大会》受到广大的关注.深圳某中学学生会就《中国诗词大会》节目的喜爱程度,在校内进行了问卷调查,并对问卷调查的结果分为“非常喜欢”、“比较喜欢”、“感觉一般”、“不太喜欢”四个等级,分别记作A、B、C、D;根据调查结果绘制出如图所示的扇形和条形统计图,请结合图中所给信息解答下列问题:
 (1)、本次被调查的对象共有人;被调查者“不太喜欢”有人;(2)、将扇形统计图和条形统计图补充完整;(3)、假设这所学校有1500名学生,请据此估计“比较喜欢”的学生有多少人?20.(1)、化简: ;(2)、先化简再求值: ,其中x=-2, .21. 阅读下面的材料:
(1)、本次被调查的对象共有人;被调查者“不太喜欢”有人;(2)、将扇形统计图和条形统计图补充完整;(3)、假设这所学校有1500名学生,请据此估计“比较喜欢”的学生有多少人?20.(1)、化简: ;(2)、先化简再求值: ,其中x=-2, .21. 阅读下面的材料:按照一定顺序排列着的一列数称为数列,数列中的每一个数叫做这个数列的项.排在第一位的数称为第一项,记为 ,排在第二位的数称为第二项,记为 ,依此类推,排在第n位的数称为第n项,记为 .所以,数列的一般形式可以写成: , , ,…, .
一般地,如果一个数列从第二项起,每一项与它前一项的差等于同一个常数,那么这个数列叫做等差数列,这个常数叫做等差数列的公差,公差通常用d表示.如:数列1,3,5,7,…为等差数列,其中 , ,公差为 .
根据以上材料,解答下列问题:
(1)、等差数列5,10,15,…的公差d为 , 第5项是 .(2)、如果一个数列 , , ,…, …,是等差数列,且公差为d,那么根据定义可得到: , , ,…, ,….所以 ,
,
,
……,
由此,请你填空完成等差数列的通项公式: ()d.
(3)、 是不是等差数列 , , …的项?如果是,是第几项?22. 某学校2019学年举行席地绘画大赛.共收到绘画作品480件,其中的优秀作品评出了一、二、三等奖.占获奖总数的几分之几
获奖作品的件数
一等奖
b
二等奖
c
三等奖
a
96
(1)、则a= ;b= ;c= ;(2)、学校决定为获一等奖同学每人购买一个书包,获得二等奖同学每人购买一个文具盒,获得三等奖同学每人购买一支钢笔,并且每位获奖同学颁发一个证书,已知文具盒单价是书包单价的 ,证书的单价是文具盒单价的 ,钢笔的单介是文具盒单价的 ,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?23. 如图,已知点A、B、C是数轴上三点,O为原点.点C对应的数为6,BC=4,AB=12. (1)、求点A、B对应的数;(2)、动点P、Q分别同时从A、C出发,分别以每秒6个单位和3个单位的速度沿数轴正方向运动.M为AP的中点,N在CQ上,且CN= CQ , 设运动时间为t(t>0).
(1)、求点A、B对应的数;(2)、动点P、Q分别同时从A、C出发,分别以每秒6个单位和3个单位的速度沿数轴正方向运动.M为AP的中点,N在CQ上,且CN= CQ , 设运动时间为t(t>0).①求点M、N对应的数(用含t的式子表示); ②t为何值时,OM=2BN .