广东省深圳市光明区2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-10-20 类型：期末考试

进入出卷网下载

一、单选题

1. 2019的相反数是（）

A、2019 B、-2019 C、 $\frac{1}{2019}$ D、 $- \frac{1}{2019}$

查看试题解析
2. 2020的绝对值等于（）

A、 2020 B、-2020 C、 $\frac{1}{2020}$ D、 $- \frac{1}{2020}$

查看试题解析
3. 光明科学城规划总面积达99000000平方米，将对标全球最高标准、最好水平.其中99000000用科学记数法表示为（）

A、 $9.9 \times 10^{7}$ B、 $99 \times 10^{7}$ C、 $9.9 \times 10^{6}$ D、 $0.99 \times 10^{8}$

查看试题解析
4. 如图，所示的几何体是由若干个大小相同的小正方体组成的，则该几何体的左视图(从左面看)是（）

A、 B、 C、 D、

查看试题解析
5. 在下列调查方式中，较为合适的是（）

A、为了解深圳市中小学生的视力情况，采用普查的方式 B、为了解龙岗区中小学生的课外阅读习惯情况，采用普查的方式 C、为了解某校七年级(2)班学生期末考试数学成绩情况，采用抽样调查方式 D、为了解我市市民对消防安全知识的了解情况，采用抽样调查的方式

查看试题解析
6. 如图，小红同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能正确解释这一现象的数学知识是（）

A、两点之间，线段最短 B、两点确定一条直线 C、过一点，有无数条直线 D、连接两点之间的线段叫做两点间的距离

查看试题解析
7. 下列各式计算正确的是（）

A、 $3^{2} = 6$ B、 ${(- \frac{1}{2})}^{3} = \frac{1}{8}$ C、 $3 a + b = 3 a b$ D、 $4 a^{3} b - 5 b a^{3} = - a^{3} b$

查看试题解析
8. 如果方程 $2 x - 6 = 0$ ，那么 $4 x + 8$ 的值（）

A、21 B、20 C、19 D、18

查看试题解析
9. 如图，已知线段AB=12cm，点N在AB上，NB=2cm，M是AB中点，那么线段MN 的长为　　　　( 　 )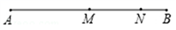

A、5cm B、4 $c m$ C、3 $c m$ D、2 $c m$

查看试题解析
10. 若 $| m - 4 | + {(n + 2)}^{2} = 0$ ，则mn的值是（）

A、16 B、-16 C、8 D、-8

查看试题解析
11.
如图，点O在直线AB上，射线OC平分∠DOB．若∠COB=35°，则∠AOD等于（　　）

A、35° B、70° C、110° D、145°

查看试题解析
12. 观察下列等式：
⑴ $1^{3} = 1^{2}$

⑵ $1^{3} + 2^{3} = 3^{2}$

⑶ $1^{3} + 2^{3} + 3^{3} = 6^{2}$

⑷ $1^{3} + 2^{3} + 3^{3} + 4^{3} = 10^{2}$

……

根据此规律，第10个等式的右边应该是 $a^{2}$ ，则a的值是（）

A、45 B、54 C、55 D、65

查看试题解析

二、填空题

13. 单项式 $- \frac{3}{7} a^{3} b^{2}$ 的次数是．

查看试题解析
14. 如图，是一个正方体纸盒的展开图，正方体的各面上标有“知识就是力量”六个字，则原正方体中与“知”字相对的字是．

查看试题解析
15. 若 $- 2 a^{6} b$ 与 $7 a^{2 m} b^{n - 2}$ 是同类项，则m=、n= ．

查看试题解析
16. 如图，将三个同样的正方形的一个顶点重合放置，如果 $∠ 1 = 50^{\circ}$ ， $∠ 3 = 30^{\circ}$ ，那么 $∠ 2$ 的度数是．

查看试题解析

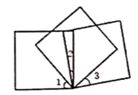
三、解答题

17. 计算

(1)、 $- 8 + 14 - 6 + 20$

(2)、 $(- \frac{1}{2} + \frac{3}{4} - \frac{5}{6}) \times (- 12)$

查看试题解析
18. 先化简，再求值： $2 m^{2} - 4 m + 1 - 2 (m^{2} + 2 m - \frac{1}{2})$ ，其中 $m = - \frac{1}{2}$

查看试题解析
19. 解方程：

(1)、 $5 (x - 3) + 3 = 2 x$

(2)、 $\frac{x + 1}{3} - 1 = \frac{2 - x}{4}$

查看试题解析
20. 保护环境，让我们从垃圾分类做起．某区环保部门为了提高宣传实效，抽样调查了部分居民小区一段时间内生活垃圾的分类情况（如图1），进行整理后，绘制了如下两幅尚不完整的统计图：

根据图表解答下列问题：

(1)、请将图2﹣条形统计图补充完整；

(2)、在图3﹣扇形统计图中，求出“D”部分所对应的圆心角等于度；

(3)、在抽样数据中，产生的有害垃圾共有吨；

(4)、调查发现，在可回收物中废纸垃圾约占 $\frac{1}{5}$ ，若每回收1吨废纸可再造好红外线0.85吨．假设该城市每月产生的生活垃圾为10000吨，且全部分类处理，那么每月回收的废纸可再造好纸多少吨？

查看试题解析
21. 某中学库存若干套桌椅，准备修理后支援贫困山区学校．现有甲、乙两木工组，甲每天修理桌椅16套，乙每天修桌椅比甲多8套，甲单独修完这些桌椅比乙单独修完多用20天，学校每天付甲组80元修理费，付乙组120元修理费．

(1)、该中学库存多少套桌椅？

(2)、在修理过程中，学校要派一名工人进行质量监督，学校负担他每天10元生活补助费，现有三种修理方案：a、由甲单独修理；b、由乙单独修理；c、甲、乙合作同时修理．你认为哪种方案省时又省钱？为什么？

查看试题解析
22. 填空，完成下列说理过程.
如图，点A、O、B在同一条直线上， $O D$ ， $O E$ 分别平分 $∠ A O C$ 和 $∠ B O C$ .

(1)、求 $∠ D O E$ 的度数：
解：如图，因为 $O D$ 是 $∠ A O C$ 的平分线，

所以 $∠ C O D = \frac{1}{2} ∠ A O C$ .

因为 $O E$ 是 $∠ B O C$ 的平分线，

所以 $∠ C O E = \frac{1}{2}$ .

所以 $∠ D O E = ∠ C O D +$ $= \frac{1}{2} (∠ A O C + ∠ B O C) = \frac{1}{2} ∠ A O B =$ $^{\circ}$ .

(2)、如果 $∠ C O D = 65^{\circ}$ ，求 $∠ A O E$ 的度数.
解：由（1）可知 $∠ D O E = 90^{\circ}$ .

因为 $∠ C O D = 65^{\circ}$

所以 $= ∠ C O D = 65^{\circ}$

则： $∠ A O E = ∠ A O D +$ $=$ $^{\circ}$ .

查看试题解析
23. 如图1，长方形 $O A B C$ 的边 $O A$ 在数轴上，O为原点，长方形 $O A B C$ 的面积为12， $O C$ 边长为3.

(1)、数轴上点A表示的数为.

(2)、将长方形 $O A B C$ 沿数轴水平移动，移动后的长方形记为 $O' A' B' C'$ ，移动后的长方形 $O' A' B' C'$ 与原长方形 $O A B C$ 重叠部分（如图2中阴影部分）的面积记为.S
设点A的移动距离 $A A' = x$ .当 $S = 4$ 时，x=.

(3)、当S恰好等于原长方形 $O A B C$ 面积的一半时，求数轴上点 $A'$ 表示的数为多少.

查看试题解析