广东省江门市恩平市2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-10-20 类型：期末考试

进入出卷网下载

一、单选题

1. 在0，1，﹣3，|﹣3|这四个数中，最小的数是（）

A、0 B、1 C、﹣3 D、|﹣3|

查看试题解析
2. 如果向东走4千米记为+4千米，那么走了﹣2千米表示（　　）

A、向东走了2千米 B、向南走了2千米 C、向西走了2千米 D、向北走了2千米

查看试题解析
3. 用科学记数法表示3080000，正确的是（）

A、 $308 \times 10^{4}$ B、 $30.8 \times 10^{5}$ C、 $3.08 \times 10^{6}$ D、 $3.8 \times 10^{6}$

查看试题解析
4. 下面运算正确的是（）

A、3ab+3ac=6abc B、4a²b-4ab²=0 C、 $2 x^{2} + 7 x^{2} = 9 x^{4}$ D、3y²-2y²=y²

查看试题解析
5. 下列不属于同类项的是（）

A、﹣1和2 B、 $x^{2} y$ 和 $6 π x^{2} y$ C、 $3 x^{2} y$ 和﹣ $3 x^{2} y$ D、 $\frac{4}{5}$ $a^{2}$ 和 $\frac{4}{5}$ $b^{2} a$

查看试题解析
6. 一个几何体的展开图如图所示，这个几何体是（）

A、三棱柱 B、三棱锥 C、四棱柱 D、四棱锥

查看试题解析
7. 方程3x﹣1＝4的解是（）

A、- $\frac{5}{3}$ B、 $\frac{5}{3}$ C、﹣1 D、1

查看试题解析
8. 下列方程中，是一元一次方程的是（　　）

A、3x+2y=5 B、y²+6y+5=0 C、 $\frac{1}{3}$ x= $\frac{1}{x}$ D、3x﹣4=7

查看试题解析
9. 下列说法中，正确的有（　　）
①经过两点有且只有一条直线；
②两点之间，直线最短；
③同角（或等角）的余角相等；
④若AB=BC，则点B是线段AC的中点．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10.
如图，将长方形纸片ABCD的∠C沿着GF折叠（点F在BC上，不与B，C重合），使点C落在长方形内部的点E处，若FH平分∠BFE，则∠GFH的度数是（　　）

A、110° B、100° C、90° D、80°

查看试题解析

二、填空题

11. 单项式﹣4xy²的系数是．

查看试题解析
12. 已知∠A＝28°35′，则∠A的余角是．

查看试题解析
13. 若a、b互为相反数，则3a+3b﹣2的值为．

查看试题解析
14. $5 x^{b} y^{8}$ 与 $- 4 x^{2} y^{a}$ 是同类项，则a+b的值是.

查看试题解析
15. 已知x＝5是方程mx﹣8＝20+m的解，则m＝．

查看试题解析
16. 如图，O是直线AB上一点，OD是∠BOC的平分线，若∠AOC＝70°，则∠BOD＝．

查看试题解析
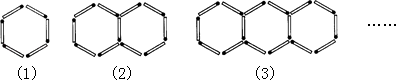
17.
用火柴棒按如图所示的方式摆图形，按照这样的规律继续摆下去，第n个图形需要根火柴棒（用含n的代数式表示）．

查看试题解析

三、解答题

18. 计算：0.25×|﹣4|﹣4÷（﹣2）²+（﹣3）× $\frac{5}{6}$ ．

查看试题解析
19. 解方程： $\frac{2 x - 1}{3} - \frac{x - 5}{6} = 1$ ．

查看试题解析
20. 统计数据显示，在我国的 $664$ 座城市中，按水资源情况可分为三类：暂不缺水城市、一般缺水城市和严重缺水城市.其中，暂不缺水城市数比严重缺水城市数的3倍多52座，一般缺水城市数是严重缺水城市数的 $2$ 倍.求严重缺水城市有多少座？

查看试题解析
21. 如图，在平面内有A，B，C三点．

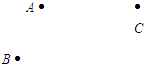
$(1)$ 画直线AC，线段BC，射线AB；

$(2)$ 在线段BC上任取一点D不同于B，C，连接线段AD；

$(3)$ 数数看，此时图中线段的条数．

查看试题解析
22. 先化简，再求值：
已知（a﹣1）²+|b+2|=0，求代数式﹣a²b+（3ab²﹣a²b）﹣2（2ab²﹣a²b）的值．

查看试题解析
23. 如图，将带有45°和30°两块直角三角尺的直角顶点C叠放在一起，

(1)、若∠DCE＝25°，则∠ACB＝；若∠ACB＝150°，则∠DCE＝；

(2)、猜想∠ACB与∠DCE的大小有何特殊关系，并说明理由．

查看试题解析
24. 现在，某商场进行促销活动，出售一种优惠购物卡（注：此卡只作为购物优惠凭证不能顶替货款），花300元买这种卡后，凭卡可在这家商场按标价的8折购物．

(1)、顾客购买多少元金额的商品时，买卡与不买卡花钱相等？在什么情况下购物合算？

(2)、小张要买一台标价为3500元的冰箱，如何购买合算？小张能节省多少元钱？

(3)、小张按合算的方案，把这台冰箱买下，如果某商场还能盈利25%，这台冰箱的进价是多少元？

查看试题解析
25.

(1)、如图1，已知AB＝12cm，点C为线段AB上的一个动点，点D、E分别是AC、BC的中点．

若点C恰为AB的中点，则DE＝cm.

若AC＝4cm，则DE＝cm.

(2)、DE的长度与点C的位置是否有关？请说明理由．

(3)、如图2，已知∠AOB＝120°，过角的内部任一点C画射线OC，若OD、OE分别是∠AOC、∠BOC的平分线，则∠DOE的大小与射线OC的位置是否有关？请说明理由．

查看试题解析