广东省广州市海珠区2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-10-20 类型：期末考试

进入出卷网下载

一、单选题

1. 2019的相反数是（）

A、2019 B、-2019 C、 $\frac{1}{2019}$ D、 $- \frac{1}{2019}$

查看试题解析
2. 如图，是一个正方体的展开图，原正方体中“文”字一面相对的面上的字是（）

A、建 B、明 C、城 D、市

查看试题解析
3. 下列代数式中，属于多项式的是（）

A、 $\frac{y}{3}$ B、 $3 x - y$ C、 $\frac{y}{x}$ D、 $- x$

查看试题解析
4. 若 $∠ A = 25 °$ ，则 $∠ A$ 的补角的度数为（）

A、 $55 °$ B、 $175 °$ C、 $75 °$ D、 $155^{°}$

查看试题解析
5. 已知 $5 x^{1 + m} y^{4}$ 与 $x^{3} y^{4}$ 是同类项，则m的值是（）

A、3 B、2 C、5 D、4

查看试题解析
6. 如果 ${(x - 2)}^{2} + | y + 1 | = 0,$ 那么 $x + y =$ （）

A、1 B、-1 C、2 D、0

查看试题解析
7. 下列判断错误的是（）

A、若 $a = b$ ，则 $a + c = b + c$ B、若 $a = b$ ，则 $a c = b c$ C、若 $a = b$ ，则 $a - c = b - c$ D、若 $a = b$ ，则 $\frac{a}{c} = \frac{b}{c}$

查看试题解析
8. 已知a，b是有理数，若a在数轴上的对应点的位置如图所示，且 $a + b < 0$ ，有以下结论：① $b < 0$ ； ② $a - b < 0$ ；③ $b < - a < a < - b$ ； ④ $| a | < | b |$ ，其中结论正确的个数是（）

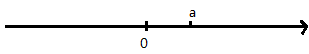A、4个 B、2个 C、3个 D、1个

查看试题解析
9. 用白铁皮做罐头盒，每张铁皮可制盒身15个或盒底42个，一个盒身与两个盒底配成一套罐头盒. 现有108张白铁皮，用多少张制盒身，多少张制盒底，可以正好制成整套罐头盒？设用 $x$ 张白铁皮制盒身，可列出方程（）

A、 $15 (108 - x) = 2 \times 42 x$ B、 $15 x = 2 \times 42 \times (108 - x)$ C、 $2 \times 15 (108 - x) = 42 x$ D、 $2 \times 15 x = 42 \times (108 - x)$

查看试题解析
10. 在数轴上，点A对应的数是-6，点B对应的数是-2，点O对应的数是0.动点P、Q分别从A、B同时出发，以每秒3个单位，每秒1个单位的速度向右运动。在运动过程中，线段PQ的长度始终是另一线段长的整数倍，这条线段是（）

A、PB B、OP C、OQ D、QB

查看试题解析

二、填空题

11. 计算 $2 \times (- 5)$ 的结果是.

查看试题解析
12. 截止2019年10月底，广州建成5G基站约12000座，多个项目列入广东省首批5G融合应用项目，将数12000用科学记数法表示，可记为-.

查看试题解析
13. 如果 $m - n = 5$ ，那么 $3 m - 3 n - 7$ 的值是.

查看试题解析
14. 若关于x的方程 $5 x + 3 k = 1$ 的解是 $x = - 1$ ，则k的值为.

查看试题解析
15. 在一次猜谜比赛中，每个选手要回答30题，答对一题得20分，不答或答错扣10分，如果小明一共得了120分，那么小明答对了题.

查看试题解析
16. 利用计算机设计了一个程序，输入和输出的结果如下表：
当输入数据是n时，输出的结果是.

查看试题解析

三、解答题

17. 计算：

(1)、 $- 5 - (- 3) + (- 2) + 8$

(2)、 ${(- 1)}^{2} \times 2 + {(- 2)}^{3} \div | - 4 |$

查看试题解析
18. 解下列方程：

(1)、5 $x = 3 (2 + x)$

(2)、 $\frac{x + 4}{2} - \frac{x + 2}{3} = 1$

查看试题解析
19. 如图，已知点A，点B，点D，点E，点F

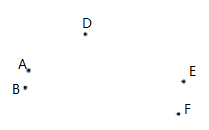(1)、作直线BE，连接AF，线段AF与直线BE交于点C，作射线CD．

(2)、在（1）所画图中，若 $∠ ACB = 20 °$ ，CD平分 $∠ ACE$ ，求 $∠ DCB$ 的大小.

查看试题解析
20. 如图，点C在线段AB的延长线上，D为AC的中点，DC=3.

(1)、求AC的长；

(2)、若AB=2BC，求AB的长

查看试题解析
21. 已知代数式 $M = 3 (a - 2 b) - (b + 2 a)$ .

(1)、化简M；

(2)、如果 $(a + 1) x^{2} + 4 x^{b - 2} - 3 = 0$ 是关于x的一元一次方程，求M的值.

查看试题解析
22. 已知关于x的一元一次方程 $4 x + 2 m = 3 x - 1$ ,

(1)、求这个方程的解；

(2)、若这个方程的解与关于x的方程 $3 (x + m) = - (x - 1)$ 的解相同，求m的值.

查看试题解析
23. 如图，有一个长方形纸条ABCD，点P，Q是线段CD上的两个动点，且点P始终在点Q左侧，在AB上有一点O，连结PO、QO，以PO，QO为折痕翻折纸条，使点A、点B、点C、点D分别落在点A’、点B’、点C’、点D’上.

(1)、当 $∠ POA = 20 °$ 时， $∠ A'OA$ = $°$

(2)、当A’O与B’O重合时， $∠ POQ$ = $°$ .

(3)、当 $∠ B^{'}O^{'}A^{'} = 30 °$ 时，求 $∠ POQ$ 的度数.

查看试题解析
24. 魔术大师夏尔 $Δ$ 巴比耶90岁时定义了一个魔法三角阵，三角阵中含有四个区域（三个“边区域”和一个“核心区域”，如图1中的阴影部分），每个区域都含有5个数，把差相同的连续九个正整数填进三角阵中，每个区域的5个数的和必须相同。例如：图2中，把相差为1的九个数（1至9）填入后，三个“边区域”及“核心区域”的数的和都是22，即6+1+9+2+4=22，4+2+8+3+5=22，5+3+7+1+6=22，2+9+1+7+3=22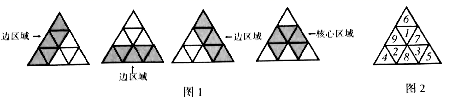

(1)、操作与发现：
在图3中，小明把差为1的连续九个正整数（1至9）分为三组，其中1、2、3为同一组，4、5、6为同一组，7、8、9为同一组，把同组数填进同一花纹的△中，生成了一个符合定义的魔法三角阵，且各区域的5个数的和为28，请你在图3中把小明的发现填写完整.

(2)、操作与应用：
根据（1）发现的结果，把差为8的连续九个正整数填进图4中，仍能得到符合定义的魔法三角阵，且各区域的5个数的和为2019.

设其中最小的数为x，则最大的数是；（用含x的式子表示）.

(3)、把图4中的9个数填写完整，并说明理由.

查看试题解析