广东省佛山市禅城区2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-10-20 类型:期末考试
一、单选题
-
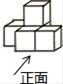
1. ﹣ 的相反数是( )A、﹣ B、﹣ C、 D、2. 如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )
 A、
A、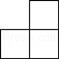 B、
B、 C、
C、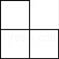 D、
D、 3. 手电筒发射出来的光线,类似于几何中的( )A、线段 B、射线 C、直线 D、折线4. 下列计算正确的是( )A、 B、 C、 D、5. 天文单位是天文学中计量天体之间距离的一种单位,其数值取地球与太阳之间的平均距离,即149597870700m,约为149600000km.将数149600000用科学记数法表示为( )A、 B、 C、 D、6. 下列调查中,最适合采用全面调查(普查)方式的是( )A、对市辖区水质情况的调查 B、对电视台“商城聚焦”栏目收视率的调查 C、对某小区每天丢弃塑料袋数量的调查 D、对你校某班学生最喜爱的运动项目的调查7. 下列运算正确的是A、 B、 C、 D、8. 若关于x的方程ax﹣4=a﹣2的解是x=3,则a的值是( )A、﹣2 B、2 C、﹣1 D、19. 如图,甲从A点出发向北偏东70°方向走到点B,乙从点A出发向南偏西15°方向走到点C,则∠BAC的度数是( )
3. 手电筒发射出来的光线,类似于几何中的( )A、线段 B、射线 C、直线 D、折线4. 下列计算正确的是( )A、 B、 C、 D、5. 天文单位是天文学中计量天体之间距离的一种单位,其数值取地球与太阳之间的平均距离,即149597870700m,约为149600000km.将数149600000用科学记数法表示为( )A、 B、 C、 D、6. 下列调查中,最适合采用全面调查(普查)方式的是( )A、对市辖区水质情况的调查 B、对电视台“商城聚焦”栏目收视率的调查 C、对某小区每天丢弃塑料袋数量的调查 D、对你校某班学生最喜爱的运动项目的调查7. 下列运算正确的是A、 B、 C、 D、8. 若关于x的方程ax﹣4=a﹣2的解是x=3,则a的值是( )A、﹣2 B、2 C、﹣1 D、19. 如图,甲从A点出发向北偏东70°方向走到点B,乙从点A出发向南偏西15°方向走到点C,则∠BAC的度数是( )
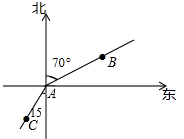 A、85° B、105° C、125° D、160°10. 如图,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )
A、85° B、105° C、125° D、160°10. 如图,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系是( )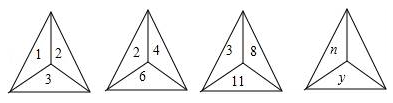 A、y=2n+1 B、y=2n+n C、y=2n+1+n D、y=2n+n+1
A、y=2n+1 B、y=2n+n C、y=2n+1+n D、y=2n+n+1二、填空题
-
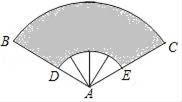
11. 如果某学生向右走10步记作+10,那么向左走5步,应记作 .12. 当x=5,y=4时,式子x- 的值是 .13. 要在墙壁上固定一根小木条,至少需要两枚钉子,其数学原理是.14. 当代数式2x﹣2与3+x的值相等时,x= .15. 学校组织植树活动,原计划的安排是在甲处有10人,在乙处有17人,去到植树现场后发现甲处的工作量比较大,决定从乙处调一部分人去支援甲处,使在甲处植树的人数是在乙处植树人数的2倍,那么应调往甲处多少人?若设应调往甲处x人,则可列方程16. 为庆祝祖国华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条AB,AC夹角为120°,AB的长为30cm,贴布部分BD的长为20cm,则贴布部分的面积约为cm2 .
 17. 如图,一个 5 ´ 5 ´ 5 的正方体,先在它的前后方向正中央开凿一个“十字形”的孔(打通),再在它的上 下方向正中央也开凿一个“十字形”的孔(打通),最后在它的左右方向正中央开凿一个“十字形”的孔(打通),这样得到一个被凿空了的几何体,则凿掉部分的体积为.
17. 如图,一个 5 ´ 5 ´ 5 的正方体,先在它的前后方向正中央开凿一个“十字形”的孔(打通),再在它的上 下方向正中央也开凿一个“十字形”的孔(打通),最后在它的左右方向正中央开凿一个“十字形”的孔(打通),这样得到一个被凿空了的几何体,则凿掉部分的体积为.
三、解答题
-
18. 计算:19. 解方程:20. 如图,在同一平面内有4个点A、B、C、D,请按要求完成下列问题.(此题作图不要求写出画法和结论)
 (1)、连接线段AB、线段AD;作直线BD、射线AC,两线相交于点O;(2)、我们容易判断出线段AB+AD与BD的数量关系是 , 理由是.21. 为了弘扬中华传统文化,某校组织八年级800名学生参加汉字听写大赛,为了了解学生整体听写能力,从中抽取部分学生的成绩(打分取正整数,满分100分)进行统计分析,得到如图所示的频数分布表:
(1)、连接线段AB、线段AD;作直线BD、射线AC,两线相交于点O;(2)、我们容易判断出线段AB+AD与BD的数量关系是 , 理由是.21. 为了弘扬中华传统文化,某校组织八年级800名学生参加汉字听写大赛,为了了解学生整体听写能力,从中抽取部分学生的成绩(打分取正整数,满分100分)进行统计分析,得到如图所示的频数分布表:

请根据尚未完成的表格,解答下列问题:
(1)、本次抽样调查,一共调查名学生的成绩,表中n=(2)、补全图中所示的频数分布直方图;(3)、若成绩超过80分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?22. 元旦放假时,小明一家三口一起乘小轿车去探望爷爷、奶奶和姥爷、姥姥.早上从家里出发,向东走了5千米到超市买东西,然后又向东走了2.5千米到爷爷家,下午从爷爷家出发向西走了10千米到姥爷家,晚上返回家里.(1)、若以小明家为原点,向东为正方向,用1个单位长度表示1千米,请将超市、爷爷家和姥爷家的位置在下面数轴上分别用点A、B、C表示出来; (2)、超市和姥爷家相距多少千米?(3)、若小轿车每千米耗油0.08升,求小明一家从出发到返回家,小轿车的耗油量.23. 小丽放学回家后准备完成下面的题目:化简(□x2﹣6x+8)+(6x﹣5x2﹣2),发现系数“□“印刷不清楚.(1)、她把“□”猜成3,请你化简(3x2﹣6x+8)+(6x﹣5x2﹣2);(2)、她妈妈说:你猜错了,我看到该题的标准答案是6.通过计算说明原题中“□”是几?24. 已知:O是直线AB上的一点, 是直角,OE平分 .
(2)、超市和姥爷家相距多少千米?(3)、若小轿车每千米耗油0.08升,求小明一家从出发到返回家,小轿车的耗油量.23. 小丽放学回家后准备完成下面的题目:化简(□x2﹣6x+8)+(6x﹣5x2﹣2),发现系数“□“印刷不清楚.(1)、她把“□”猜成3,请你化简(3x2﹣6x+8)+(6x﹣5x2﹣2);(2)、她妈妈说:你猜错了,我看到该题的标准答案是6.通过计算说明原题中“□”是几?24. 已知:O是直线AB上的一点, 是直角,OE平分 . (1)、如图1.若 .求 的度数;(2)、在图1中, ,直接写出 的度数(用含a的代数式表示);
(1)、如图1.若 .求 的度数;(2)、在图1中, ,直接写出 的度数(用含a的代数式表示);
(3)、
将图1中的 绕顶点O顺时针旋转至图2的位置,探究 和 的度数之间的关系.写出你的结论,并说明理由.
25. 如图1,P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米,如果P、Q同时出发,用t(秒)表示移动时间,那么: (1)、如图1,若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP(2)、如图2,点Q在CA上运动,试求出t为何值时,三角形QAB的面积等于三角形ABC面积的 ;(3)、如图3,当P点到达C点时,P、Q两点都停止运动,试求当t为何值时,线段AQ的长度等于线段BP的长的
(1)、如图1,若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP(2)、如图2,点Q在CA上运动,试求出t为何值时,三角形QAB的面积等于三角形ABC面积的 ;(3)、如图3,当P点到达C点时,P、Q两点都停止运动,试求当t为何值时,线段AQ的长度等于线段BP的长的