吉林省长春市德惠市2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-10-20 类型:期末考试
一、单选题
-
1. ﹣8的立方根是( )A、2 B、﹣2 C、4 D、﹣0.52. 下列命题中,为假命题的是( )A、等腰三角形是轴对称图形 B、三角形的外角大于它的一个内角 C、三角形的中线是一条线段 D、两边及其夹角分别相等的两三角形全等3. 若a·2·23=28 , 则a等于( )A、4 B、8 C、16 D、324. 某人将一枚质地均匀的硬币连续抛10次,落地后正面朝上6次,反面朝上4次,则下列说法正确的是( )A、出现正面的频率是6 B、出现正面的频率是60% C、出现正面的频率是4 D、出现正面的频率是40%5. 根据下列条件,能画出唯一△ABC的是( )A、AB=3,∠A=60°,∠B=40° B、AB=3,BC=4,∠A=40° C、AB=3,BC=4,AC=8 D、AB=3,∠C=90°6. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
 A、
A、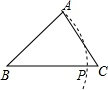 B、
B、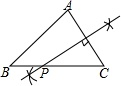 C、
C、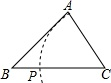 D、
D、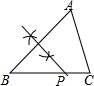 7. 如图所示,在边长为 a 的正方形中挖去一个边长为 b 的 小正方形 (a > b) ,再把剩余的部分剪拼成一个矩形,通过计算图形(阴影部分)的面积,验证了一个等式是( )
7. 如图所示,在边长为 a 的正方形中挖去一个边长为 b 的 小正方形 (a > b) ,再把剩余的部分剪拼成一个矩形,通过计算图形(阴影部分)的面积,验证了一个等式是( ) A、a2 - b2 = (a + b)(a - b) B、(a + b) 2 = a2 + 2ab + b2 C、(a - b) 2 = a2 - 2ab + b2 D、(a + 2b)(a - b) = a2 + ab - 2b28. 如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm.A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )
A、a2 - b2 = (a + b)(a - b) B、(a + b) 2 = a2 + 2ab + b2 C、(a - b) 2 = a2 - 2ab + b2 D、(a + 2b)(a - b) = a2 + ab - 2b28. 如图是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm.A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )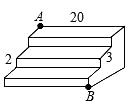 A、 dm B、20dm C、25dm D、35dm
A、 dm B、20dm C、25dm D、35dm二、填空题
-
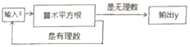
9. 计算:24a3b2÷3ab= .10. 如图,有一个数值转换器,流程如下,当输入的x为256时,输出的y是.
 11. 如图,在方格纸中,以AB为一边做△ABP,使之与△ABC全等,从 P1 , P2 , P3 , P4,四个点中,满足条件的点P有个
11. 如图,在方格纸中,以AB为一边做△ABP,使之与△ABC全等,从 P1 , P2 , P3 , P4,四个点中,满足条件的点P有个 12. 已知一个三角形的三条边的长分别为 、 和 ,那么这个三角形的最大内角的大小为度.13. 如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,则∠CDB的大小为度.
12. 已知一个三角形的三条边的长分别为 、 和 ,那么这个三角形的最大内角的大小为度.13. 如图,在△ABC中,AB=AC.以点C为圆心,以CB长为半径作圆弧,交AC的延长线于点D,连结BD.若∠A=32°,则∠CDB的大小为度.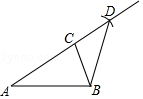 14. 《九章算术》是我国古代重要的数学著作之一,在“勾股”中记载了一道“折竹抵地”问题:“今有竹高一丈,未折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程求出AC的长为 .
14. 《九章算术》是我国古代重要的数学著作之一,在“勾股”中记载了一道“折竹抵地”问题:“今有竹高一丈,未折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程求出AC的长为 .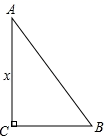
三、解答题
-
15. 把下列各数填在相应的大括号内:
,﹣0.31,﹣(﹣2),﹣ ,1.732, ,0, ,1.1010010001…(每两个1之间依次多一个0)
正分数:{…}
无理数:{…}
16. 因式分解:5x2﹣10x+517. 先化简,再求值: ,其中 .18. 图①、图②均是5×6的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、E、F均在格点上.在图①、图②中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.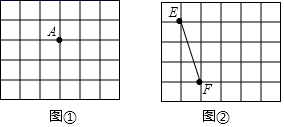 (1)、在图①中画一个正方形ABCD,使其面积为5.(2)、在图②中画一个等腰△EFG,使EF为其底边.19. 如图,在梯形ABCD中,AD∥BC,E为CD中点,连接AE并延长AE交BC的延长线于点F.
(1)、在图①中画一个正方形ABCD,使其面积为5.(2)、在图②中画一个等腰△EFG,使EF为其底边.19. 如图,在梯形ABCD中,AD∥BC,E为CD中点,连接AE并延长AE交BC的延长线于点F.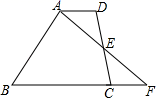 (1)、求证:CF=AD.(2)、若AD=3,AB=8,当BC为多少时,点B在线段AF的垂直平分线上,为什么?20. 在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查(每位同学必选且只选一项).下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)、求证:CF=AD.(2)、若AD=3,AB=8,当BC为多少时,点B在线段AF的垂直平分线上,为什么?20. 在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查(每位同学必选且只选一项).下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题: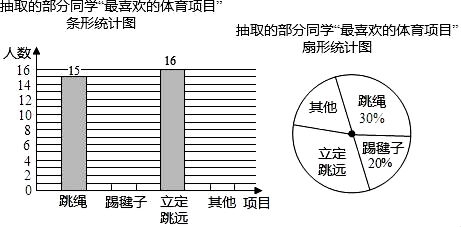 (1)、小龙一共抽取了名学生.(2)、补全条形统计图;(3)、求“其他”部分对应的扇形圆心角的度数.21. 定义 为二阶行列式,规定它的运算法则为: =ad﹣bc,例如: =5×8﹣6×7=﹣2.(1)、求 的值.(2)、若 =24,求m的值.22. 如图,在四边形ABCD中,∠BAD=∠B=∠C=90 ,AD=BC=20,AB=DC=16.将四边形ABCD沿直线AE折叠,使点D落在BC边上的点F处.
(1)、小龙一共抽取了名学生.(2)、补全条形统计图;(3)、求“其他”部分对应的扇形圆心角的度数.21. 定义 为二阶行列式,规定它的运算法则为: =ad﹣bc,例如: =5×8﹣6×7=﹣2.(1)、求 的值.(2)、若 =24,求m的值.22. 如图,在四边形ABCD中,∠BAD=∠B=∠C=90 ,AD=BC=20,AB=DC=16.将四边形ABCD沿直线AE折叠,使点D落在BC边上的点F处. (1)、求BF的长;(2)、求CE的长.23. 教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
(1)、求BF的长;(2)、求CE的长.23. 教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.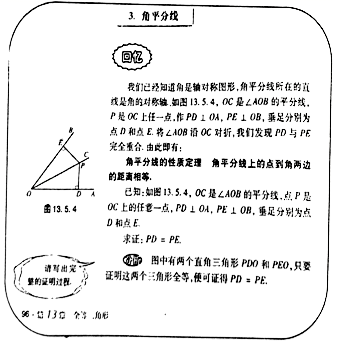
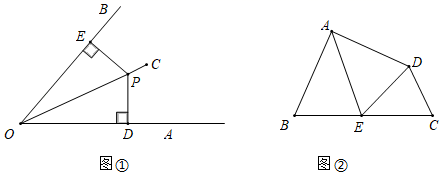 (1)、请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.(2)、求证:BE=CE.(3)、若四边形ABCD的周长为24,BE=2,面积为30,则△ABE的边AB的高的长为 .24. 如图,在△ABC中,∠BAC=90°,AB=5cm,BC=13cm,点D在线段AC上,且CD=7cm,动点P从距B点15cm的E点出发,以每秒2cm的速度沿射线EA的方向运动,时间为t秒.
(1)、请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.(2)、求证:BE=CE.(3)、若四边形ABCD的周长为24,BE=2,面积为30,则△ABE的边AB的高的长为 .24. 如图,在△ABC中,∠BAC=90°,AB=5cm,BC=13cm,点D在线段AC上,且CD=7cm,动点P从距B点15cm的E点出发,以每秒2cm的速度沿射线EA的方向运动,时间为t秒.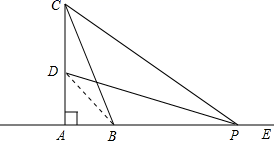 (1)、求AD的长.(2)、用含有t的代数式表示AP的长.(3)、在运动过程中,是否存在某个时刻,使△ABC与△ADP全等?若存在,请求出t值;若不存在,请说明理由.(4)、直接写出t=秒时,△PBC为等腰三角形.
(1)、求AD的长.(2)、用含有t的代数式表示AP的长.(3)、在运动过程中,是否存在某个时刻,使△ABC与△ADP全等?若存在,请求出t值;若不存在,请说明理由.(4)、直接写出t=秒时,△PBC为等腰三角形.