吉林省长春市新区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-10-20 类型:期末考试
一、填空题
-
1. 的平方根是( )A、 B、 C、 D、2. 下列是无理数的是( )A、 B、 C、 D、3. 下列运算正确的是( )A、x2+x2=x4 B、(a﹣1)2=a2﹣1 C、a2•a3=a5 D、3x+2y=5xy4. 某青年足球队的14名队员的年龄如表:
年龄(单位:岁) 19 20 21 22 人数(单位:人) 3 7 2 2 则出现频数最多的是( )
A、19岁 B、20岁 C、21岁 D、22岁5. 如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成右边的矩形.根据图形的变化过程写出的一个正确的等式是( )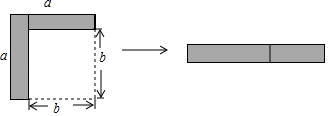 A、(a﹣b)2=a2﹣2ab+b2 B、a(a﹣b)=a2﹣ab C、(a﹣b)2=a2﹣b2 D、a2﹣b2=(a+b)(a﹣b)6.
A、(a﹣b)2=a2﹣2ab+b2 B、a(a﹣b)=a2﹣ab C、(a﹣b)2=a2﹣b2 D、a2﹣b2=(a+b)(a﹣b)6.如图,下列条件中,不能证明△ABC≌△DCB的是( )
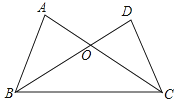 A、AB=DC,AC=DB B、AB=DC,∠ABC=∠DCB C、BO=CO,∠A=∠D D、AB=DC,∠DBC=∠ACB7. 如图,在△ABC中,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.图中等腰三角形的个数为( )
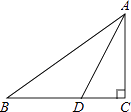
A、AB=DC,AC=DB B、AB=DC,∠ABC=∠DCB C、BO=CO,∠A=∠D D、AB=DC,∠DBC=∠ACB7. 如图,在△ABC中,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.图中等腰三角形的个数为( )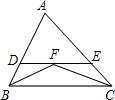 A、4 B、3 C、2 D、18. 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,则AB,AC,CE的长度关系为( )
A、4 B、3 C、2 D、18. 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,则AB,AC,CE的长度关系为( )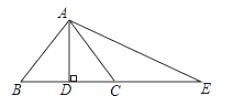 A、AB>AC=CE B、AB=AC>CE C、AB>AC>CE D、AB=AC=CE
A、AB>AC=CE B、AB=AC>CE C、AB>AC>CE D、AB=AC=CE二、填空题
-
9. 已知△ABC的三边长分别是6cm、8cm、10cm,则△ABC的面积是10. 若计算(x﹣2)(3x+m)的结果中不含关于字母x的一次项,则m的值为 .11. 有以下两个命题:①实数与数轴上的点一一对应;②﹣5没有立方根,其中是假命题的为(填序号).12. 在直角△ABC中,∠C=90°,AD平分∠BAC交BC于点D,若CD=4,则点D到斜边AB的距离为 .
 13. 学校开展综合实践活动,某班进行了小制作评比,评委们把同学们上交作品的件数按组统计,绘制了如图所示的条形统计图,小长方形的高之比为2:5:2:1,现已知第二组上交的作品件数是20,则此班这次上交的作品共件.
13. 学校开展综合实践活动,某班进行了小制作评比,评委们把同学们上交作品的件数按组统计,绘制了如图所示的条形统计图,小长方形的高之比为2:5:2:1,现已知第二组上交的作品件数是20,则此班这次上交的作品共件.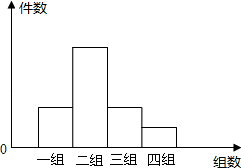 14. 如图,以Rt△ABC的三边向外作正方形,其面积分别为S1 , S2 , S3 , 且S1=6,S3=15,则S2= .
14. 如图,以Rt△ABC的三边向外作正方形,其面积分别为S1 , S2 , S3 , 且S1=6,S3=15,则S2= .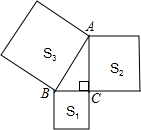
三、解答题
-
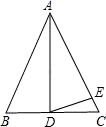
15. 计算: .16. 计算:(﹣8ab2)(﹣ a)3 .17. 如图,在△ABC中,AB=AC,AD⊥BC,∠BAD=28°,且AD=AE,求∠EDC的度数.
 18. 先化简,再求值: (x-2)2-(x+3)(x-3).其中x=- .19. 图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A和点B在小正方形的顶点上.
18. 先化简,再求值: (x-2)2-(x+3)(x-3).其中x=- .19. 图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A和点B在小正方形的顶点上.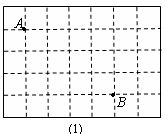
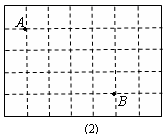 (1)、在图1中画出△ABC,使△ABC为直角三角形(点C在小正方形的顶点上,画出一个即可);(2)、在图2中画出△ABD,使△ABD为等腰三角形(点D在小正方形的顶点上,画出一个即可).20. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于 EF长为半径作圆弧,两条圆弧交于点P,连接AP,交CD于点M,若∠ACD=110°,求∠CMA的度数.
(1)、在图1中画出△ABC,使△ABC为直角三角形(点C在小正方形的顶点上,画出一个即可);(2)、在图2中画出△ABD,使△ABD为等腰三角形(点D在小正方形的顶点上,画出一个即可).20. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于 EF长为半径作圆弧,两条圆弧交于点P,连接AP,交CD于点M,若∠ACD=110°,求∠CMA的度数.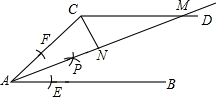 21. 在△ABC中,AB=AC,∠A=36°,CD平分∠ACB交AB于点D,DE⊥AC交AC于点E,若BD=7,且△BDC的周长为29,求AE的长.
21. 在△ABC中,AB=AC,∠A=36°,CD平分∠ACB交AB于点D,DE⊥AC交AC于点E,若BD=7,且△BDC的周长为29,求AE的长. 22. 某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取
22. 某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取 进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图: 运动项目
频数(人数)
羽毛球
30
篮球
 a
a乒乓球
36
排球
b
足球
12

请根据以上图表信息解答下列问题:
(1)、频数分布表中的a= , b=;(2)、在扇形统计图中,“排球”所在的扇形的圆心角为度;(3)、全校有多少名学生选择参加乒乓球运动?23. 张老师在一次“探究性学习”课中,设计了如下数表:n
2
3
4
5
…
a
22-1
32-1
42-1
52-1
…
b
4
6
8
10
…
c
22+1
32+1
42+1
52+1
…
(1)、请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a= , b= , c=;
(2)、猜想:以a,b,c为边的三角形是否为直角三角形并证明你的猜想.24. 如图,Rt△ABC中,∠ACB=90°,BC=30cm,AC=40cm,点D在线段AB上从点B出发,以2cm/s的速度向终点A运动,设点D的运动时间为t(s).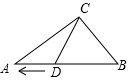 (1)、用含t的代数式表示BD的长;(2)、求AB的长;(3)、求AB边上的高;(4)、当△BCD为等腰三角形时,求t的值
(1)、用含t的代数式表示BD的长;(2)、求AB的长;(3)、求AB边上的高;(4)、当△BCD为等腰三角形时,求t的值