吉林省长春汽车经济技术开发区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-20 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 $a^{2} \cdot a$ 的结果是（）

A、 $a$ B、 $a^{2}$ C、 $a^{3}$ D、 $2 a^{3}$

查看试题解析
2. 在xy， $\frac{x}{2}, \frac{1}{3}$ ，（x+y）， $\frac{2 x y}{x + y}$ 这四个有理式中，分式是（）

A、xy B、 $\frac{x}{2}$ C、 $\frac{1}{3}$ （x+y） D、 $\frac{2 x y}{x + y}$

查看试题解析
3. 某校对1200名女生的身高进行了测量，身高在 $1 .58 m \sim 1 .63 m$ ，这一小组的频率为 $0.25$ ，则该组的人数为（）

A、150人 B、300人 C、600人 D、900人

查看试题解析
4. 解分式方程 $\frac{1}{x - 1} = \frac{2}{x^{2} - 1}$ 时，去分母化为一元一次方程，正确的是（　　）

A、x+1＝2（x﹣1） B、x﹣1＝2（x+1） C、x﹣1＝2 D、x+1＝2

查看试题解析
5. 用反证法证明“在△ABC中，如果∠B≠∠C，那么AB≠AC“时，应假设（）

A、AB＝AC B、∠B＝∠C C、AB≠AC D、∠B≠∠C

查看试题解析
6. 如图，在边长为1个单位长度的小正方形组成的网格中，点A、B都是格点，则线段AB的长度为（）

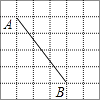A、5 B、6 C、7 D、25

查看试题解析
7. 如图，已知一条线段的长度为a，作边长为a的等边三角形的方法是：①画射线AM；②连结AC、BC；③分别以A、B为圆心，以a的长为半径作圆弧，两弧交于点C；④在射线AM上截取AB＝a；以上画法正确的顺序是（）

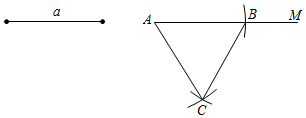A、①②③④ B、①④③② C、①④②③ D、②①④③

查看试题解析
8. 如图，在△ABC中，∠C＝90°，AD是△ABC的一条角平分线．若AC＝6，AB＝10，则点D到AB边的距离为（）

A、2 B、2.5 C、3 D、4

查看试题解析

二、填空题

9. 计算：（ $\frac{1}{3}$ ）⁰×10^﹣¹＝．

查看试题解析
10. 分解因式： $9 x^{2} - y^{2} =$ ．

查看试题解析
11. 人体内某种细胞可近似地看作球体，它的直径为0.000 000 156m，将0.000 000 156用科学记数法表示为

查看试题解析
12. 若长方形的面积为a²+a，长为a+ab，则宽为．

查看试题解析
13. 如图，在 $Δ A B C$ 中， $D$ 为边 $B C$ 的中点， $D E ⊥ A B$ 于点 $E$ ， $D F ⊥ A C$ 于点 $F$ ，且 $B E = C F$ ．若 $∠ B D E = 30 °$ ，则 $∠ A$ 的大小为度．

查看试题解析
14. 如图，在 $Δ A B C$ 中， $A B = A C$ ，点 $D$ 、 $E$ 在 $B C$ 的延长线上， $G$ 是 $A C$ 上一点，且 $C G = C D$ ， $F$ 是 $G D$ 上一点，且 $D F = D E$ ．若 $∠ A = 100 °$ ，则 $∠ E$ 的大小为度．

查看试题解析
15. 如图，有一张长方形纸片 $A B C D$ ， $A B = 4$ ， $A D = 3$ ．先将长方形纸片 $A B C D$ 折叠，使边 $A D$ 落在边 $A B$ 上，点 $D$ 落在点 $E$ 处，折痕为 $A F$ ；再将 $Δ A E F$ 沿 $E F$ 翻折， $A F$ 与 $B C$ 相交于点 $G$ ，则 $F G$ 的长为．

查看试题解析

三、解答题

16. 解方程： $\frac{x}{2 x - 1} + \frac{5}{1 - 2 x} = 2$

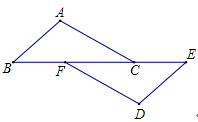
查看试题解析
17. 计算：

(1)、（﹣2a）²•（a﹣1）

(2)、 $(\frac{3}{m^{- 4}} - \frac{24}{m^{2} - 16}) \div (\frac{m}{m + 4})$

查看试题解析
18. 如图，点B，F，C，E在一条直线上，∠A=∠D，AC=DF，且AC∥DF.求证：△ABC≌△DEF.

查看试题解析
19. 图①、图②均是6×6的正方形网格，每个小正方形的顶点叫做格点，每个小正方形的边长均为1．

(1)、在图①中，以格点为端点，画线段MN＝ $\sqrt{37}$ ．

(2)、在图②中，以格点为顶点，画正方形ABCD，使它的面积为10．

查看试题解析
20. 为建国70周年献礼，某灯具厂计划加工9000套彩灯。为尽快完成任务，实际每天加工彩灯的数量是原计划的1.2倍，结果提前5天完成任务。求该灯具厂原计划每天加工这种彩灯的数量。

查看试题解析
21. 如图，某中学校园内有一块长为（3a+b）米，宽为（2a+b）米的长方形地块，学校计划在中间留一块边长为（a+b）米的正方形地块修建一座雕像，然后将阴影部分进行绿化.

(1)、求绿化的面积.（用含a、b的代数式表示）

(2)、当a＝2，b＝4时，求绿化的面积.

查看试题解析
22. 某中学为丰富综合实践活动，开设了四个实验室如下：A．物理；B．化学；C．信息；D．生物．为了解学生最喜欢哪个实验室，随机抽取了部分学生进行调查，每位被调查的学生都选择了一个自己最喜欢的实验室，调查后将调查结果绘制成了如图统计图，请根据统计图回答下列问题

(1)、求这次被调查的学生人数．

(2)、请将条形统计图补充完整．

(3)、求出扇形统计图中B对应的圆心角的度数．

查看试题解析
23.

(1)、教材呈现：下图是华师版八年级上册数学教材第94页的部分内容．

定理证明：请根据教材中的分析，结合图①，写出“线段垂直平分线的性质定理”完整的证明过程．

定理应用：

(2)、如图②，在 $Δ A B C$ 中，直线 $m$ 、 $n$ 分别是边 $B C$ 、 $A C$ 的垂直平分线，直线 $m$ 、 $n$ 的交点为 $O$ ．过点 $O$ 作 $O H ⊥ A B$ 于点 $H$ ．求证： $A H = B H$ ．

(3)、如图③，在 $Δ A B C$ 中， $A B = B C$ ，边 $A B$ 的垂直平分线 $l$ 交 $A C$ 于点 $D$ ，边 $B C$ 的垂直平分线 $k$ 交 $A C$ 于点 $E$ ．若 $∠ A B C = 120 °$ ， $A C = 15$ ，则 $D E$ 的长为．

查看试题解析
24. 如图，在△ABC中，AB＝50cm，BC＝30cm，AC＝40cm．

(1)、求证：∠ACB＝90°

(2)、求AB边上的高．

(3)、点D从点B出发在线段AB上以2cm/s的速度向终点A运动，设点D的运动时间为t（s）．
①BD的长用含t的代数式表示为．

②当△BCD为等腰三角形时，t= ．

查看试题解析