吉林省吉林市永吉县2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-20 类型：期末考试

进入出卷网下载

一、单选题

1. 某红外线遥控器发出的红外线波长为0.000 000 94 m，0.000 000 94用科学记数法表示应为（）

A、0.94×10^－⁶ B、9.4×10^－⁷ C、94×10^－⁸ D、9.4×10^－⁶

查看试题解析
2. 下列图形中，是轴对称图形的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列运算错误的是（）

A、 ${(2 b^{3})}^{2} = 4 b^{9}$ B、 $a^{2} \cdot a^{3} = a^{5}$ C、 ${(a^{2})}^{3} = a^{6}$ D、 $a^{3} \div a^{2} = a (a \neq 0)$

查看试题解析
4. 一个等腰三角形的两边长分别为3 cm和7 cm，则此三角形的周长为（）

A、13 cm B、17 cm C、7 cm或13 cm D、不确定

查看试题解析
5. 如图，已知∠1＝∠2，要使△ABD≌△ACD，需从下列条件中增加一个，错误的选法是（）

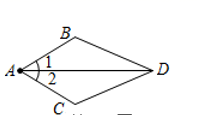A、∠ADB＝∠ADC B、∠B＝∠C C、AB＝AC D、DB＝DC

查看试题解析
6. 如图，△ABC中，AB=AC，∠B=40°．把△ABC的边AC对折，使顶点C和点A重合，折痕交BC于D，连接AD，则∠BAD的度数为（）

A、50° B、55° C、60° D、65°

查看试题解析

二、填空题

7. 若分式 $\frac{| x | - 1}{x + 1}$ 的值为零，则x的值为．

查看试题解析
8. 已知一个正多边形的一个外角为45°，则它的内角和为度．

查看试题解析
9. 计算： $(- 2 a^{2} b c) \div (- a b)$ = ．

查看试题解析
10. 已知a-b=4，ab=6，则 $a^{2} + b^{2}$ = ．

查看试题解析
11. 如图，在△ABC中，AB=AC，BD是△ABC的一条角平分线，若∠A =36°，则∠BDC的度数为．

查看试题解析
12. 若a-b=1，则 $a^{2} - b^{2} - 2 b$ 的值为．

查看试题解析
13. 如图，在△ABC中，AB=AC，∠BAC=120°，D为BC上一点，DA⊥AC，AD=24 cm，则BC的长cm．

查看试题解析
14. 如图（1）是长方形纸条，∠DEF=20°，将纸条沿EF折叠成如图（2），则图（2）中的∠CFG的度数是．

查看试题解析

三、解答题

15. 计算： $| 3 - \sqrt{5} | - {(\frac{1}{2})}^{- 1} - {(- 2)}^{0}$ ．

查看试题解析
16. 某同学化简a（a+2b）﹣（a+b）（a﹣b）出现了不符合题意，解答过程如下：
原式=a²+2ab﹣（a²﹣b²）（第一步）

=a²+2ab﹣a²﹣b²（第二步）

=2ab﹣b²（第三步）

(1)、该同学解答过程从第几步开始出错，不符合题意原因是什么；

(2)、写出此题正确的解答过程．

查看试题解析
17. 如图， $D$ 是 $A B$ 上一点， $D F$ 交 $A C$ 于点 $E$ ， $D E = F E$ ， $F C / / A B$ ，求证： $A E = C E$ .

查看试题解析
18. A，B两种机器人都被用来搬运化工原料，A型机器人比B型机器人每小时多搬运30kg，A型机器人搬运900kg与B型机器人搬运600kg所用时间相等，两种机器人每小时分别搬运多少化工原料？

查看试题解析
19. 一次课堂练习，小红做了如下四道因式分解题：① $x^{2} - y^{2} = (x - y) (x + y)$ ；② $a^{3} - a = a (a^{2} - 1)$ ；③ $x^{2} y - x y^{2} = x y (x - y)$ ；④ $2 m^{2} + 4 m n + 2 n^{2} = {(2 m + 2 n)}^{2}$

(1)、小红做错的或不完整的题目是（填序号）；

(2)、把（1）题中题目的正确答案写在下面．

查看试题解析
20. 已知方程 $\frac{x - 3}{x - 2} + 1 = \frac{m}{2 - x}$ ①．

(1)、若x=1是方程的解，则m的值为；

(2)、若m=1，解方程．

查看试题解析
21. 如图，在4×4的正方形方格中，阴影部分是涂黑5个小正方形所形成的图案．若再将方格内空白的两个小正方形涂黑，使得到的新阴影图案成为一个轴对称图形，请在下面的备用图中画出具有不同对称轴的两个图案，并画出对称轴．

查看试题解析
22. 先化简 $\frac{2 x + 4}{x^{2} - 1} \div \frac{x + 2}{x^{2} - 2 x + 1} - \frac{2 x}{x + 1}$ ，然后在-2，-1，0，1中选择一个适当的数代入求值．

查看试题解析
23. 如图，AD，BC相交于点O，AC=BD，∠C=∠D=90°．

(1)、求证：OA=OB；

(2)、若∠ABC=30°，OC=5，求BC的长．

查看试题解析
24. 阅读下列材料：利用完全平方公式，可以将多项式 $a x^{2} + b x + c (a \neq 0)$ 变形为 $a {(x + m)}^{2} + n$ 的形式，我们把这种变形方法，叫做配方法．运用配方法及平方差公式能对一些多项式进行因式分解．例如： $x^{2} + 11 x + 24 = x^{2} + 11 x + {(\frac{11}{2})}^{2} - {(\frac{11}{2})}^{2} + 24 = {(x + \frac{11}{2})}^{2} - \frac{25}{4} = (x + \frac{11}{2} + \frac{5}{2}) (x + \frac{11}{2} - \frac{5}{2})$ 根据以上材料，解答下列问题：

(1)、用配方法将 $x^{2} + 8 x - 1$ 化成 ${(x + m)}^{2} + n$ 的形式，则 $x^{2} + 8 x - 1 =$ ；

(2)、用配方法和平方差公式把多项式 $x^{2} - 2 x - 8$ 进行因式分解；

(3)、对于任意实数x，y，多项式 $x^{2} + y^{2} - 2 x - 4 y + 16$ 的值总为（填序号）．
①正数②非负数③0

查看试题解析
25. 某商店经销一种纪念品，11月份的营业额为2000元．为扩大销售，12月份该商店对这种纪念品打九折销售，结果销售量增加20件，营业额增加700元．

(1)、求这种纪念品11月份的销售单价；

(2)、11月份该商店销售这种商品件；

(3)、若11月份销售这种纪念品获利800元，求12月份销售这种纪念品获利多少元？

查看试题解析
26. 如图，在△ABC中，AB=BC=AC=20cm．动点P，Q分别从A，B两点同时出发，沿三角形的边匀速运动．已知点P，点Q的速度都是2cm/s，当点P第一次到达B点时，P，Q两点同时停止运动．设点P的运动时间为t（s）．

(1)、∠A=度；

(2)、当0＜t＜10，且△APQ为直角三角形时，求t的值；

(3)、当△APQ为等边三角形时，直接写出t的值．

查看试题解析