吉林省白山市长白县2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-20 类型：期末考试

进入出卷网下载

一、单选题

1. 在坐标平面上有一个轴对称图形，其中A（3，﹣ $\frac{5}{2}$ ）和B（3，﹣ $\frac{11}{2}$ ）是图形上的一对对称点，若此图形上另有一点C（﹣2，﹣9），则C点对称点的坐标是（）

A、（﹣2，1） B、（﹣2，﹣ $\frac{3}{2}$ ） C、（﹣ $\frac{3}{2}$ ，﹣9） D、（﹣2，﹣1）

查看试题解析
2. 要使分式 $\frac{x + 2}{(x + 2) (x - 1)}$ 有意义，x的取值应满足（）

A、x≠1 B、x≠﹣2 C、x≠1或x≠﹣2 D、x≠1且x≠﹣2

查看试题解析
3. 下列从左边到右边的变形，是正确的因式分解的是（）

A、 $(x + 1) (x - 1) = x^{2} - 1$ B、 $x^{2} - 4 y^{2} = (x + 4 y) (x - 4 y)$ C、 $x^{2} - 2 x + 1 = x (x - 2) + 1$ D、 $x^{2} - 6 x + 9 = {(x - 3)}^{2}$

查看试题解析
4. 如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A的坐标是（a，b），经过第2019次变换后所得的点A的坐标是（）

A、（﹣a，b） B、（﹣a，﹣b） C、（a，﹣b） D、（a，b）

查看试题解析
5. 设a，b是实数，定义*的一种运算如下：a*b＝（a+b）² ，则下列结论有：①a*b＝0，则a＝0且b＝0；②a*b＝b*a；③a*（b+c）＝a*b+a*c；④a*b＝（﹣a）*（﹣b）.正确的有（）个．

A、1 B、2 C、3 D、4

查看试题解析
6. 如图， $∠ A O B = α$ ，点 $P$ 是 $∠ A O B$ 内的一定点，点 $M ， N$ 分别在 $O A 、 O B$ 上移动，当 $Δ P M N$ 的周长最小时， $∠ M P N$ 的值为（）

A、 $90^{\circ} + α$ B、 $90^{\circ} + \frac{1}{2} α$ C、 $180^{\circ} - α$ D、 $180^{\circ} - 2 α$

查看试题解析

二、填空题

7. 如图，OC平分∠AOB，D为OC上一点，DE⊥OB于E，若DE＝7，则D到OA的距离为．

查看试题解析
8. $\frac{2}{3 x^{2} (x - y)}$ 、 $\frac{1}{2 x - 2 y}$ 、 $\frac{3}{4 x y}$ 的公分母是 .

查看试题解析
9. 已知a、b、c为△ABC的三边，化简：|a+b﹣c|-|a﹣b﹣c|+|a﹣b+c|=.

查看试题解析
10. 如图，平面内有五个点，以其中任意三个点为顶点画三角形，最多可以画个三角形．

查看试题解析
11. 如图点C，D在AB同侧，AD=BC，添加一个条件就能使△ABD≌△BAC。

查看试题解析
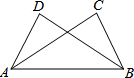12. 一个正n边形的一个外角等于72°，则n的值等于．

查看试题解析
13. 等腰三角形的两边长分别是3和7，则其周长为．

查看试题解析
14. 已知三角形的三边分别为a,b,c ，其中a ， b满足 $\sqrt{a^{2} - 6 a + 9} + \sqrt{b - 4} = 0$ ，那么这个三角形的第三边c的取值范围是.

查看试题解析
15. 如果x²+mx+6＝（x﹣2）（x﹣n），那么m+n的值为．

查看试题解析
16. 代数式（x﹣2）⁰÷ $\frac{x}{x - 1}$ 有意义，则x的取值范围是．

查看试题解析

三、解答题

17. 运用乘法公式计算：（2x﹣1）（2x+1）﹣（x﹣6）（4x+3）．

查看试题解析
18. 先化简，再求值：1﹣ $\frac{x - 2 y}{x + y}$ ÷ $\frac{x^{2} - 4 x y + 4 y^{2}}{x^{2} - y^{2}}$ ，其中x＝﹣2，y＝ $\frac{1}{2}$ ．

查看试题解析
19. 分解因式：（m+1）（m﹣9）+8m．

查看试题解析
20. 计算：（﹣ $\frac{1}{3}$ ）^﹣2+4×（﹣1）²⁰¹⁹﹣|﹣2³|+（π﹣5）⁰

查看试题解析
21. 如图，在平面直角坐标系中，△ABC的三个顶点的位置如图所示．

(1)、若△ABC内有一点P（a，b）随着△ABC平移后到了点P′（a+4，b﹣1），直接写出A点平移后对应点A′的坐标．

(2)、直接作出△ABC关于y轴对称的△A′B′C′（其中A′、B′、C′分别是A、B、C的对应点）

(3)、求四边形ABC′C的面积．

查看试题解析
22. 如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF.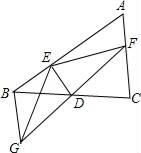

(1)、求证：BG＝CF；

(2)、请你判断BE+CF与EF的大小关系，并说明理由.

查看试题解析
23. 列方程解应用题：
中华优秀传统文化是中华民族的“根”和“魂”.为传承优秀传统文化，某校购进《西游记》和《三国演义》若干套，其中每套《西游记》的价格比每套《三国演义》的价格多40元，用3200元购买《三国演义》的套数是用2400元购买《西游记》套数的2倍，求每套《三国演义》的价格.

查看试题解析
24. “转化”是数学中的一种重要思想，即把陌生的问题转化成熟悉的问题，把复杂的问题转化成简单的问题，把抽象的问题转化为具体的问题．

(1)、请你根据已经学过的知识求出下面星形图（1）中∠A+∠B+∠C+∠D+∠E的度数；

(2)、若对图（1）中星形截去一个角，如图（2），请你求出∠A+∠B+∠C+∠D+∠E+∠F的度数；

(3)、若再对图（2）中的角进一步截去，你能由题（2）中所得的方法或规律，猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗？只要写出结论，不需要写出解题过程）

查看试题解析
25. Rt△ABC中，∠C＝90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点．令∠PDA＝∠1，∠PEB＝∠2，∠DPE＝∠α．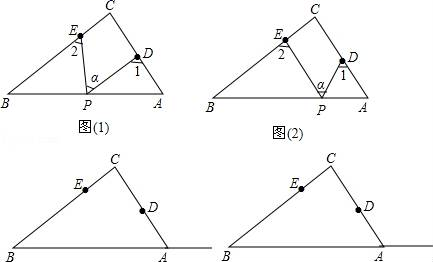

(1)、若点P在线段AB上，如图（1）所示，且∠α＝50°，则∠1+∠2＝°；

(2)、若点P在边AB上运动，如图（2）所示，则∠α、∠1、∠2之间有何关系？

(3)、若点P在Rt△ABC斜边BA的延长线上运动（CE＜CD），则∠α、∠1、∠2之间有何关系？猜想并说明理由．

查看试题解析