广东省深圳市福田区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中最大的是（）

A、1 B、 $- \sqrt{2}$ C、3 D、 $| - \frac{1}{2} |$

查看试题解析
2. 下列实数是无理数的是（）

A、 $\sqrt{4}$ B、 $\frac{4}{7}$ C、2π D、0.1010010001

查看试题解析
3. 袁隆平海水稻科研团队为考察最近选育的水稻生长情况，在同一时期，分别从甲、乙、丙三种稻苗中随机抽取部分稻苗测量苗高（单位：cm），算得它们的方差分别为 $s_{甲}^{2} = 2.7$ ， $s_{乙}^{2} = 3.4$ ， $s_{丙}^{2} = 5.3$ ，则下列对苗高的整齐程度描述正确的是（）

A、甲最整齐 B、乙最整齐 C、丙最整齐 D、一样整齐

查看试题解析
4. 下列各组数中，不能作为直角三角形的三边长的是（）

A、1， $\sqrt{3}$ ，2 B、7，12，15 C、3，4，5 D、5，12，13

查看试题解析
5. 在平面直角坐标系中，点A的坐标为（1，-3），则点A关于 $y$ 轴对称点的坐标是（）

A、（-1，-3） B、（-3，1 ） C、（1，3） D、（-1，3 ）

查看试题解析
6. 如图，将三角板的直角顶点放在直尺的一边 $B C$ 上（ $A D$ ∥ $B C$ ），若∠1=25°，则∠2的度数为（）

A、55° B、25° C、60° D、65°

查看试题解析
7. 如图，一次函数 $y = k x + b$ 的图象经过点（2，0），则下列结论正确的是（）

A、 $k > 0$ B、关于 $x$ 方程 $k x + b = 0$ 的解是 $x = 2$ C、 $b < 0$ D、y随x的增大而增大

查看试题解析
8. 若 $\sqrt{{(b - 3)}^{2}} + | a - 4 | = 0$ ，则化简 $\sqrt{\frac{a}{b}}$ 的结果是（）

A、 $\frac{2 \sqrt{3}}{3}$ B、 $\pm \frac{2 \sqrt{3}}{3}$ C、 $\frac{4 \sqrt{3}}{3}$ D、 $\pm \frac{4 \sqrt{3}}{3}$

查看试题解析
9. 下列命题是真命题的是（）

A、如果 $a^{2} = b^{2}$ ，那么 $a = b$ B、0的平方根是0 C、如果 $∠ A$ 与 $∠ B$ 是内错角，那么 $∠ A = ∠ B$ D、三角形的一个外角等于它的两个内角之和

查看试题解析
10. 如图，在△ $A B C$ 中， $D$ 为 $A C$ 边上一点，以点 $A$ 为圆心， $A D$ 为半径画弧，交 $B A$ 的延长线于点 $E$ ，连接 $E D$ .若 $∠ C = 50 °$ ， $∠ B = 60 °$ ，则 $∠ C D E$ 的度数为（）

A、 $130 °$ B、 $135 °$ C、 $140 °$ D、 $145 °$

查看试题解析
11. 我国明代数学家程大位所著的《算法统宗》中记载了一道有趣的题目：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”题目大意是：100个和尚分100个馒头，刚好分完，大和尚1人分3个馒头，小和尚3人分一个馒头，问大、小和尚各有多少人？若大和尚有 $x$ 人，小和尚有 $y$ 人，则下列方程或方程组中:① ${\begin{cases} x + y = 100 ， \\ \frac{1}{3} x + 3 y = 100 ； \end{cases}$ ② ${\begin{cases} x + y = 100 ， \\ 3 x + \frac{1}{3} y = 100 ； \end{cases}$ ③ $3 x + \frac{1}{3} (100 - x) = 100 ；$ ④ $\frac{1}{3} (100 - y) + 3 y = 100.$ 正确的是（）

A、①③ B、①④ C、②③ D、②④

查看试题解析
12. 如图，在长方形 $A B C D$ 中， $A B$ =4， $B C$ =8，点 $E$ 是 $B C$ 边上一点，且 $A E = E C$ ，点 $P$ 是边 $A D$ 上一动点，连接 $P E$ ， $P C$ ，则下列结论：① $B E = 3$ ；②当 $A P = 5$ 时， $P E$ 平分 $∠ A E C$ ； ③△ $P E C$ 周长的最小值为15 ；④当 $A P = \frac{25}{6}$ 时， $A E$ 平分 $∠ B E P$ .其中正确的个数有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

13. 36的算术平方根是

查看试题解析
14. 深圳市某中学对该校八年级学生进行了体育测试，下表是某学习小组10名学生的测试成绩，则这组学生体育平均成绩是分.

成绩（分）

45

48

50

人数

2

5

3

查看试题解析
15. 我们规定：当 $k$ ， $b$ 为常数（ $k \neq 0$ ， $b \neq 0$ ）时，称 $y = k x + b$ 与 $y = \frac{1}{k} x + \frac{1}{b}$ 互为倒数函数.例如： $y = 3 x - 5$ 的倒数函数是 $y = \frac{1}{3} x - \frac{1}{5}$ .则在平面直角坐标系中，函数 $y = 2 x - 4$ 与它倒数函数两者图象的交点坐标为.

查看试题解析
16. 如图，在Rt△ $A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C = 4$ ，点 $E$ 在 $A C$ 上，且 $A E = 1$ ，连接 $B E$ ， $∠ B E F = 90 °$ ，且 $B E = F E$ ，连接 $C F$ ，则 $C F$ 的长为.

查看试题解析

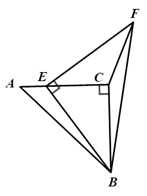
三、解答题

17. 计算: $\sqrt{48} + \sqrt{12} (\sqrt{3} - 2) - \sqrt[3]{- 8}$ .

查看试题解析
18. 解二元一次方程组： ${\begin{matrix} 3 x + 2 y = 7 ， \\ x - y = 4 . \end{matrix}$

查看试题解析
19. 某校在“垃圾分类”宣传培训后，对学生知晓情况进行了一次测试，其测试成绩按照标准划分为四个等级：A优秀，B良好，C合格，D不合格.为了了解该校学生的成绩状况，对在校学生进行随机抽样调查，调查结果绘制成了以下两幅不完整的统计图：

请结合统计图回答下列问题：

(1)、该校抽样调查的学生人数为人；

(2)、请补全条形统计图；

(3)、样本中，学生成绩的中位数所在等级是；（填“A”、“B”、“C”或“D”）

(4)、该校共有学生3000人，估计全校测试成绩为优秀和良好的学生共有人.

查看试题解析
20. 深圳市某小区为了以崭新的面貌迎接“创文”工作，决定请甲、乙两个装饰公司对小区外墙进行装饰维护.若由甲、乙两个公司合作，需8天完成，小区需支付费用12.8万元；若由甲公司单独做4天后，剩下的由乙公司来做，还需10天才能完成，小区需支付费用12.4万元.问：甲、乙两个装饰公司平均每天收取的费用分别是多少万元？

查看试题解析
21. 在△ABC中，AD平分∠BAC交BC于点D，在AB上取一点E，使得EA=ED.

(1)、求证：DE∥AC；

(2)、若ED=EB，BD=2，EA=3，求AD的长.

查看试题解析
22. 甲、乙两车先后从“深圳书城”出发，沿相同的路线到距书城240km的某市.因路况原因，甲车行驶的路程y（km）与甲车行驶的时间x（h）的函数关系图象为折线O-A-B，乙车行驶的路程y（km）与甲车行驶的时间x（h）的函数关系图象为线段CD.

(1)、求线段AB所在直线的函数表达式；

(2)、①乙车比甲车晚出发多少小时；
②乙车出发多少小时后追上甲车？

(3)、乙车出发多少小时后甲、乙两车相距10千米？

查看试题解析
23. 如下图，已知直线 $y = x - 4$ 分别与 $x$ 轴， $y$ 轴交于 $A$ ， $B$ 两点，直线 $O G$ ： $y = k x (k < 0)$ 交 $A B$ 于点 $D$ .

(1)、求 $A$ ， $B$ 两点的坐标；

(2)、如图1，点E是线段OB的中点，连结AE，点F是射线OG上一点，当 $O G ⊥ A E$ ，且 $O F = A E$ 时，求 $E F$ 的长；

(3)、如图2，若 $k = - \frac{4}{3}$ ，过 $B$ 点作 $B C$ ∥ $O G$ ，交 $x$ 轴于点 $C$ ，此时在 $x$ 轴上是否存在点 $M$ ，使 $∠ A B M + ∠ C B O = 45 °$ ，若存在，求出点 $M$ 的坐标；若不存在，请说明理由.

查看试题解析

成绩（分）	45	48	50
人数	2	5	3