广东省清远市英德市2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，是无理数的为（）

A、3.14 B、 $\frac{1}{3}$ C、 $\sqrt{3}$ D、 $\sqrt{9}$

查看试题解析
2. 在平面直角坐标系中，下列各点位于x轴上的是（）

A、（1，﹣2） B、（3，0） C、（﹣1，3） D、（0，﹣4）

查看试题解析
3. 一次函数y＝﹣2x+2的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 方程2x+y=5与下列方程构成的方程组的解为 ${\begin{matrix} x = 3 \\ y = - 1 \end{matrix}$ 的是（）

A、x﹣y=4 B、x+y=4 C、3x﹣y=8 D、x+2y=﹣1

查看试题解析
5. 已知两数x，y之和是10，且x比y的2倍大3，则下列所列方程组正确的值是（）

A、 ${\begin{array}{l} x + y = 10 \\ y = 2 x + 3 \end{array}$ B、 ${\begin{array}{l} x + y = 10 \\ y = 2 x - 3 \end{array}$ C、 ${\begin{array}{l} x + y = 10 \\ x = 2 y + 3 \end{array}$ D、 ${\begin{array}{l} x + y = 10 \\ x = 2 y - 3 \end{array}$

查看试题解析
6. 某小组长统计组内5人一天在课堂上的发言次数分別为3，3，0，4，5.关于这组数据，下列说法错误的是（）

A、众数是3 B、中位数是0 C、平均数3 D、方差是2.8

查看试题解析
7. 下列命题中，是真命题的是（）

A、0的平方根是它本身 B、1的算术平方根是﹣1 C、 $\sqrt{\frac{1}{2}}$ 是最简二次根式 D、有一个角等于60°的三角形是等边三角形

查看试题解析
8. 如图， $A B / / C D$ ， $B E$ 交 $C D$ 于点 $F$ ， $∠ B = 48 °$ ， $∠ E = 20 °$ ，则 $∠ D$ 的度数为（）．

A、 $28^{\circ}$ B、 $20^{\circ}$ C、 $48^{\circ}$ D、 $68^{\circ}$

查看试题解析
9. 如图，两个较大正方形的面积分别为225，289，则字母A所代表的正方形的面积为（）

A、4 B、8 C、16 D、64

查看试题解析
10. 如图所示，下列推理及括号中所注明的推理依据错误的是（）

A、∵∠1＝∠3，∴AB∥CD（内错角相等，两直线平行） B、∵AB∥CD，∴∠1＝∠3（两直线平行，内错角相等） C、∵AD∥BC，∴∠BAD+∠ABC＝180°（两直线平行，同旁内角互补） D、∵∠DAM＝∠CBM，∴AB∥CD（两直线平行，同位角相等）

查看试题解析

二、填空题

11. 8的立方根是．

查看试题解析
12. 方程组 ${\begin{array}{l} x = 1 \\ x + y = 5 \end{array}$ 的解是．

查看试题解析
13. 写出一个平面直角坐标系中第三象限内点的坐标：（）．

查看试题解析
14. 如果一次函数y＝x﹣3的图象与y轴交于点A，那么点A的坐标是．

查看试题解析
15. 在Rt△ABC中，∠C＝90°，如果AB＝15，AC＝12，那么Rt△ABC的面积是．

查看试题解析
16. 如图，点F是△ABC的边BC延长线上一点，DF⊥AB于点D，∠A＝30°，∠F＝40°，∠ACF的度数是．

查看试题解析
17. 甲、乙两车同时从A地出发，以各自的速度匀速向B地行驶．甲车先到达B地后，立即按原路以相同速度匀速返回（停留时间不作考虑），直到两车相遇．若甲、乙两车之间的距离y（千米）与两车行驶的时间x（小时）之间的函数图象如图所示，则A，B两地之间的距离为千米．

查看试题解析

三、解答题

18. 计算： $(\sqrt{24} - \sqrt{6}) \div \sqrt{3}$

查看试题解析
19. 解方程组： ${\begin{array}{l} 2 x - y = 3 \\ 3 x - y = 8 \end{array}$

查看试题解析
20. 如图，在平面直角坐标系中，Rt△ABC的三个顶点坐标为A（﹣3，0），B（﹣3，﹣3），C（﹣1，﹣3）．

(1)、在图中作出△ABC关于x轴对称的图形△DEF；

(2)、求线段DF的长．

查看试题解析
21. 在开展“学雷锋社会实践”活动中，某校为了解全校1000名学生参加活动的情况，随机调查了50名学生每人参加活动的次数，并根据数据绘成如图的条形统计图：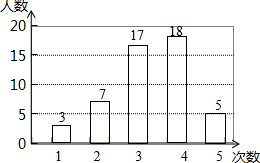

(1)、这50个样本数据的中位数是次，众数是次；

(2)、求这50个样本数据的平均数；

(3)、根据样本数据，估算该校1000名学生大约有多少人参加了4次实践活动．

查看试题解析
22. 某电器公司计划装运甲、乙两种家电到农村销售（规定每辆汽车按规定满载，且每辆汽车只能装同一种家电），已知每辆汽车可装运甲种家电20台，乙种家电30台．

(1)、若用8辆汽车装运甲、乙两种家电共190台到A地销售，问装运甲、乙两种家电的汽车各有多少辆？

(2)、如果每台甲种家电的利润是180元，每台乙种家电的利润是300元，那么该公司售完这190台家电后的总利润是多少？

查看试题解析
23. 如图，在平面直角坐标系中，点O是坐标系原点，在△AOC中，OA＝OC，点A坐标为（﹣3，4），点C在x轴的正半轴上，直线AC交y轴于点M，将△AOC沿AC折叠得到△ABC，请解答下列问题：

(1)、点C的坐标为；

(2)、求直线AC的函数关系式；

(3)、求点B的坐标．

查看试题解析
24. 如图，CD∥EF，AC⊥AE，且∠α和∠β的度数满足方程组 ${\begin{array}{l} 2 ∠ α + ∠ β = 235 ° \\ ∠ β - ∠ α = 70 ° \end{array}$

(1)、求∠α和∠β的度数．

(2)、求证：AB∥CD．

(3)、求∠C的度数．

查看试题解析
25. 如图，在平面直角坐标系中，过点A（0，6）的直线AB与直线OC相交于点C（2，4）动点P沿路线O→C→B运动．

(1)、求直线AB的解析式；

(2)、当△OPB的面积是△OBC的面积的 $\frac{1}{4}$ 时，求出这时点P的坐标；

(3)、是否存在点P，使△OBP是直角三角形？若存在，直接写出点P的坐标，若不存在，请说明理由．

查看试题解析