广东省梅州市五华县2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-20 类型：期末考试

进入出卷网下载

一、单选题

1. 若直角三角形两直角边长分别为5和12，则斜边的长为（）

A、17 B、7 C、14 D、13

查看试题解析
2. 下列各式中，正确的是 $()$

A、 $\sqrt{4} = \pm 2$ B、 $\pm \sqrt{9} = 3$ C、 $\sqrt{{(- 3)}^{2}} = - 3$ D、 $\sqrt[3]{- 27} = - 3$

查看试题解析
3. 下列各数：3.141，，，，，0.1010010001……，其中无理数有（）

A、1个 B、2 C、3个 D、4个

查看试题解析
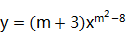4. 已知是正比例函数，则m的值是（）

A、8 B、4 C、±3 D、3

查看试题解析
5. 若 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ 是下列某二元一次方程组的解，则这个方程组为（）

A、 ${\begin{array}{l} x + 3 y = 5 \\ x + y = 1 \end{array}$ B、 ${\begin{array}{l} 2 x - y = 5 \\ x + y = 1 \end{array}$ C、 ${\begin{array}{l} x = 2 y \\ x = 3 y + 1 \end{array}$ D、 ${\begin{array}{l} x = y - 3 \\ y + 2 x = 5 \end{array}$

查看试题解析
6. 式子 $\sqrt{x + 2}$ 在实数范围内有意义，则x的取值范围是（）

A、x＞﹣2 B、x≥﹣2 C、x＜﹣2 D、x≤﹣2

查看试题解析
7. 如图，AB∥CD，∠2＝36°，∠3＝80°，则∠1的度数为（）

A、54° B、34° C、46° D、44°

查看试题解析
8. 对一组数据：2，1，3，2，3分析错误的是（）

A、平均数是2.2 B、方差是4 C、众数是3和2 D、中位数是2

查看试题解析
9. 若 $| 3 x - 2 y - 1 | + \sqrt{x + y - 2} = 0$ ，则点（x，y）在第（）象限．

A、四 B、三 C、二 D、一

查看试题解析
10. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m，先到终点的人原地休息．已知甲先出发2s．在跑步过程中，甲、乙两人的距离y（m）与乙出发的时间t（s）之间的关系如图所示，给出以下结论：①a＝8；②b＝92；③c＝123．其中正确的是（）

A、①②③ B、仅有①② C、仅有①③ D、仅有②③

查看试题解析

二、填空题

11. 已知点M $(3, - 2)$ 关于y轴的对称点为N（a，b），则a+b的值是．

查看试题解析
12. $\frac{4}{9}$ 的平方根为

查看试题解析
13. 已知函数y=-3x+1的图象经过点 $A (- 1 ， y_{1})$ 、 $B (1 ， y_{2})$ ，则 $y_{1}$ $y_{2}$ （填“ ”，“ ”或“ ”）.

查看试题解析
14. 如图，下列推理：①若∠1=∠2，则 $AB / / CD$ ；②若 $AB / / CD$ 则∠3=∠4；③若 $∠ A B C + ∠ B C D = 180^{°}$ ，则 $AD / / BC$ ；④若∠1=∠2，则 $∠ ADB = ∠ CBD$ 。其中正确的个数是（填序号）。

查看试题解析
15. 已知关于x，y的二元一次方程组 ${\begin{array}{l} x + 2 y = m \\ 2 x + y = 4 \end{array}$ 的解满足x﹣y＝3，则m的值为

查看试题解析
16. 已知等腰△ABC中，底边BC＝20，D为AB上一点，且CD＝16，BD＝12，则△ABC的周长为．

查看试题解析
17. 如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动一个单位，依次得到点P₁（0，1）；P₂（1，1）；P₃（1，0）；P₄（1，﹣1）；P₅（2，﹣1）；P₆（2，0）……，则点P₂₀₁₉的坐标是．

查看试题解析

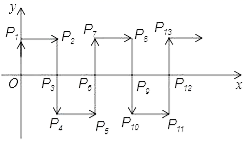
三、解答题

18. 计算： ${(1 - \sqrt{2})}^{0} + {(\frac{1}{2})}^{- 1} - \sqrt{8} \div \sqrt{2} + | \sqrt{2} - 2 |$

查看试题解析
19. 解方程组 ${\begin{array}{l} 2 x - y = 4 \\ 3 x + 2 y = 6 \end{array}$ $\begin{array}{l} ① \\ ② \end{array}$

查看试题解析
20. 如图，在直角坐标系中， $A (- 1 ， 5)$ ， $B (- 1 ， 0)$ ， $C (- 4 ， 3)$ ．

(1)、求 $Δ A B C$ 的面积；

(2)、若把 $Δ A B C$ 向下平移2个单位，再向右平移5个单位得到 $Δ A^{'} B^{'} C^{'}$ ，请画出 $Δ A^{'} B^{'} C^{'}$ 并写出 $C^{'}$ 的坐标．

查看试题解析
21. 在慈善一日捐活动中，学校团总支为了了解本校学生的捐款情况，随机抽取了50名学生的捐款数进行了统计，并绘制成下面的统计图.

(1)、这50名同学捐款的众数为元，中位数为元；

(2)、该校共有600名学生参与捐款，请估计该校学生的捐款总数.

查看试题解析
22. 某校组织“大手拉小手，义卖献爱心”活动，计划购买黑白两种颜色的文化衫进行手绘设计后出售，并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花4800元购买了黑白两种颜色的文化衫200件，每件文化衫的批发价及手绘后的零售价如表：

批发价(元)

零售价(元)

黑色文化衫

25

45

白色文化衫

20

35

(1)、学校购进黑.白文化衫各几件？

(2)、通过手绘设计后全部售出，求该校这次义卖活动所获利润.

查看试题解析
23. 如图，在△ABC中，AC＝21，BC＝13，D是AC边上一点，BD＝12，AD＝16．

(1)、求证：BD⊥AC．

(2)、若E是边AB上的动点，求线段DE的最小值．

查看试题解析
24. 已知点A（0，4）、C（﹣2，0）在直线l：y＝kx+b上，l和函数y＝﹣4x+a的图象交于点B。

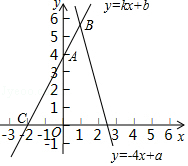(1)、求直线l的表达式；

(2)、若点B的横坐标是1，求关于x、y的方程组 ${\begin{matrix} y = k x + b \\ y = - 4 x + a \end{matrix}$ 的解及a的值．

(3)、若点A关于x轴的对称点为P，求△PBC的面积．

查看试题解析
25. 已知，直线AB∥CD．

(1)、如图1，若点E是AB、CD之间的一点，连接BE.DE得到∠BED．求证：∠BED＝∠B+∠D．

(2)、若直线MN分别与AB、CD交于点E.F．
①如图2，∠BEF和∠EFD的平分线交于点G．猜想∠G的度数，并证明你的猜想；

②如图3，EG₁和EG₂为∠BEF内满足∠1＝∠2的两条线，分别与∠EFD的平分线交于点G₁和G₂ ．求证：∠FG₁E+∠G₂＝180°．

查看试题解析

	批发价(元)	零售价(元)
黑色文化衫	25	45
白色文化衫	20	35