广东省广州市越秀区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-20 类型：期末考试

进入出卷网下载

一、单选题

1. 已知一个三角形两边的长分别是 $2$ 和 $5$ ，那么第三边的边长可能是下列各数中的（）

A、 $1$ B、 $2$ C、 $3$ D、 $5$

查看试题解析
2. 如图，已知∠ABC＝∠BAD ，添加下列条件还不能判定△ABC≌△BAD的是（）

A、AC＝BD B、∠CAB＝∠DBA C、∠C＝∠D D、BC＝AD

查看试题解析
3. 下列运算正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 $a^{3} \div a = a^{3}$ C、 $a^{2} \cdot a^{3} = a^{5}$ D、 ${(a^{2})}^{4} = a^{6}$

查看试题解析
4. 要使分式 $\frac{5 x}{x + 3}$ 有意义，则 $x$ 的取值范围是（）

A、 $x \neq - 3$ B、 $x \neq 3$ C、 $x \neq 0$ D、 $x \neq \pm 3$

查看试题解析
5. 下列变形从左到右一定正确的是（）．

A、 $\frac{a}{b} = \frac{a - 2}{b - 2}$ B、 $\frac{a}{b} = \frac{a c}{b c}$ C、 $\frac{a x}{b x} = \frac{a}{b}$ D、 $\frac{a}{b} = \frac{a^{2}}{b^{2}}$

查看试题解析
6. 如图所示，要使一个六边形木架在同一平面内不变形，至少还要再钉上（）根木条.

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
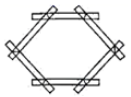7. 如图，用尺规作出∠AOB的角平分线OE，在作角平分线过程中，用到的三角形全等的判定方法是（）

A、ASA B、SSS C、SAS D、AAS

查看试题解析
8. 若等腰三角形中的一个外角等于 $130 °$ ，则它的顶角的度数是（）

A、 $50 °$ B、 $80 °$ C、 $65 °$ D、 $50 °$ 或 $80 °$

查看试题解析
9. 如图， $A D / / B C$ ， $B G$ ， $A G$ 分别平分 $∠ A B C$ 与 $∠ B A D$ ， $G H ⊥ A B$ ， $G H = 5$ ，则 $A D$ 与 $B C$ 之间的距离是（）

A、 $5$ B、 $8$ C、 $10$ D、 $15$

查看试题解析
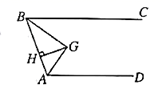10. 若 $a$ ， $b$ ， $c$ 是 $Δ A B C$ 的三边长，且 $a^{2} + b^{2} + c^{2} - a b - a c - b c = 0$ ，则 $Δ A B C$ 的形状是（）

A、等腰三角形 B、等腰直角三角形 C、等边三角形 D、不能确定

查看试题解析

二、填空题

11. 一个多边形的内角和是1800°，这个多边形是边形．

查看试题解析
12. 若关于x的多项式 $x^{2} + 10 x + k$ （ $k$ 为常数是完全平方式，则k=.

查看试题解析
13. 分式 $\frac{3}{2 a^{3} b^{2} c}$ 与 $\frac{a - b}{6 a^{2} b^{4} c}$ 的最简公分母是．

查看试题解析
14. 若3^m＝5，3ⁿ＝8，则3^2m+n＝.

查看试题解析
15. 点 $(- 3, 4)$ 与点 $(a^{2}, b^{2})$ 关于 $y$ 轴对称，则 $(a + b) (a - b) =$ .

查看试题解析
16. 如图， $Δ A B C$ 是等边三角形， $A D = \frac{1}{3} A B$ ，点 $E$ 、 $F$ 分别为边 $A C$ 、 $B C$ 上的动点，当 $Δ D E F$ 的周长最小时， $∠ F D E$ 的度数是.

查看试题解析

三、解答题

17. 解方程： $\frac{3}{x + 1} = \frac{x}{x - 1} - 1$ .

查看试题解析
18. 计算：

(1)、 ${(- 2 x)}^{3} - 3 x (x - 2 x^{2})$

(2)、 $[{(x + 2 y)}^{2} - (x - 2 y) (x + 2 y)] \div 4 y$

查看试题解析
19. 分解因式：

(1)、 $a - 6 a b + 9 a b^{2}$

(2)、 $x^{2} (x - y) + y^{2} (y - x)$

查看试题解析
20. 如图所示，在△ABC中，D是BC边上一点∠1＝∠2，∠3＝∠4，∠BAC＝69°，求∠DAC的度数．

查看试题解析
21.

(1)、先化简再求值： $(1 - \frac{x}{x + 1}) \div \frac{2}{x^{2} - 1}$ ，其中 $x = - 3$ ；

(2)、如果 $a^{2} + 2 a - 1 = 0$ ，求代数式 $(a - \frac{4}{a}) \cdot \frac{a^{2}}{a - 2}$ 的值.

查看试题解析
22. 如图， $P$ 是 $O C$ 上一点， $P D ⊥ O A$ 于 $D$ ， $P E ⊥ O B$ 于 $E$ . $F$ 、 $G$ 分别是 $O A$ 、 $O B$ 上的点，且 $P F = P G$ ， $D F = E G$ .

(1)、求证： $O C$ 是 $∠ A O B$ 的平分线.

(2)、若 $P F / / O B$ ，且 $P F = 8$ ， $∠ A O B = 30 °$ ，求 $P E$ 的长.

查看试题解析
23. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ，点 $P$ 是直线 $A C$ 上的动点（不和 $A$ 、 $C$ 重合）， $C D ⊥ B P$ 于点 $D$ ，交直线 $A B$ 于点 $Q$ .

(1)、当点 $P$ 在边 $A C$ 上时，求证： $A P = A Q$

(2)、若点 $P$ 在 $A C$ 的延长线上时，（1）的结论是否成立？若成立，请画出图形（不写画法，画出示意图）；若不成立，请直接写出符合题意结论.

查看试题解析
24. 春节前夕，某超市用 $6000$ 元购进了一批箱装饮料，上市后很快售完，接着又用 $8800$ 元购进第二批这种箱装饮料.已知第二批所购箱装饮料的进价比第一批每箱多 $20$ 元，且数量是第一批箱数的 $\frac{4}{3}$ 倍.

(1)、求第一批箱装饮料每箱的进价是多少元；

(2)、若两批箱装饮料按相同的标价出售，为加快销售，商家决定最后的 $10$ 箱饮料按八折出售，如果两批箱装饮料全部售完利润率不低于 $36 %$ （不考虑其他因素），那么每箱饮料的标价至少多少元？

查看试题解析
25. 如图所示，点 $O$ 是线段 $A C$ 的中点， $O B ⊥ A C$ ， $O A = 9$ .

(1)、如图1，若 $∠ A B O = 30 °$ ，求证 $Δ A B C$ 是等边三角形；

(2)、如图1，在（1）的条件下，若点 $D$ 在射线 $A C$ 上，点 $D$ 在点 $C$ 右侧，且 $Δ B D Q$ 是等边三角形， $Q C$ 的延长线交直线 $O B$ 于点 $P$ ，求 $P C$ 的长度；

(3)、如图2，在（1）的条件下，若点 $M$ 在线段 $B C$ 上， $Δ O M N$ 是等边三角形，且点 $M$ 沿着线段 $B C$ 从点 $B$ 运动到点 $C$ ，点 $N$ 随之运动，求点 $N$ 的运动路径的长度.

查看试题解析