广东省广州市荔湾区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-20 类型：期末考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{x + 3}{x - 2}$ 的值为 $0$ ，则 $x$ 的值为（）

A、 $x = - 3$ B、 $x = 2$ C、 $x \neq - 3$ D、 $x \neq 2$

查看试题解析
2. 下列计算正确的是（）

A、a²+a³=a⁵ B、a²•a³=a⁶ C、（a²）³=a⁶ D、（ab）²=ab²

查看试题解析
3. 下列因式分解结果正确的是（）

A、x²+3x+2=x（x+3）+2 B、4x²﹣9=（4x+3）（4x﹣3） C、a²﹣2a+1=（a+1）² D、x²﹣5x+6=（x﹣2）（x﹣3）

查看试题解析
4. 以下四家银行的行标图中，是轴对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 等腰三角形的一个角为50°，则这个等腰三角形的底角为（）

A、65° B、65°或80° C、50°或65° D、40°

查看试题解析
6. 三角形的三边长可以是（）

A、2，11，13 B、5，12，7 C、5，5，11 D、5，12，13

查看试题解析
7. 如图若△ABE≌△ACF，且AB=5，AE=2，则EC的长为（）

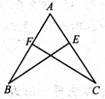A、2 B、3 C、4 D、5

查看试题解析
8. 如图，等腰△ABC的周长为21，底边BC＝5，AB的垂直平分线DE交AB于点D ，交AC于点E ，则△BEC的周长为（）

A、13 B、16 C、8 D、10

查看试题解析
9.
已知，如图，在△ABC中，OB和OC分别平分∠ABC和∠ACB，过O作DE∥BC，分别交AB、AC于点D、E，若BD+CE=5，则线段DE的长为（　　）

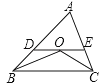A、5 B、6 C、7 D、8

查看试题解析

二、填空题

10. 如图， $△ A B C$ 中， $∠ B A C = 60 °$ ， $∠ B A C$ 的平分线 $A D$ 与边 $B C$ 的垂直平分线 $M D$ 相交于 $D$ ， $D E ⊥ A B$ 交 $A B$ 的延长线于 $E$ ， $D F ⊥ A C$ 于 $F$ ，现有下列结论：
① $D E = D F$ ；② $D E + D F = A D$ ；③ $D M$ 平分 $∠ E D F$ ；④ $A B + A C = 2 A E$ ．其中正确的有．（填写序号）

查看试题解析
11. 要使分式 $\frac{1}{x + 2}$ 有意义，则x的取值范围为．

查看试题解析
12. 若 $x^{2} + m x + 16 = {(x + n)}^{2}$ ，则常数 $m =$ .

查看试题解析
13. 如图，在△ABC中，AD、AE分别是边BC上的中线与高，AE＝4，△ABC的面积为12，则CD的长为．

查看试题解析
14. 如果多边形的每个内角都等于 $150 °$ ，则它的边数为.

查看试题解析
15. 已知m+2n﹣2＝0，则2^m•4ⁿ的值为．

查看试题解析
16. 如图，在△ABC中，AB＝AC＝5，BC＝6，AD是∠BAC的平分线，AD＝4．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是．

查看试题解析

三、解答题

17. 计算：

(1)、 $\frac{1}{3 x}$ •（6x²y）²；

(2)、（a+b）²+b（a﹣b）．

查看试题解析
18. 分解因式：

(1)、ax²﹣9a；

(2)、4ab²﹣4a²b﹣b³ ．

查看试题解析
19. 计算：

(1)、 $\frac{x + 3}{x + 2} + \frac{2 - x}{x^{2} - 4}$ ；

(2)、 $\frac{x^{2} + 2 x + 1}{x^{2} + 2 x} \div (1 - \frac{1}{x + 2})$ ．

查看试题解析
20.
如图，已知点B，E，C，F在一条直线上，AB=DF，AC=DE，∠A=∠D．

(1)、求证：AC∥DE；

(2)、若BF=13，EC=5，求BC的长．

查看试题解析
21. 如图，在平面直角坐标系中，A（2，4），B（3，1），C（﹣2，﹣1）．

(1)、在图中作出△ABC关于x轴的对称图形△A₁B₁C₁ ，并写出点A₁ ， B₁ ， C₁的坐标；

(2)、求△ABC的面积．

查看试题解析
22. 列方程解应用题：
初二（1）班组织同学乘大巴车前往爱国教育基地开展活动，基地离学校有60公里，队伍12：00从学校出发，张老师因有事情，12：15从学校自驾小车以大巴1.5倍的速度追赶，追上大巴后继续前行，结果比队伍提前15分钟到达基地，问：

(1)、大巴与小车的平均速度各是多少？

(2)、张老师追上大巴的地点到基地的路程有多远？

查看试题解析
23. 如图，在△ABC中，AB=AC=18cm，BC=10cm，AD=2BD．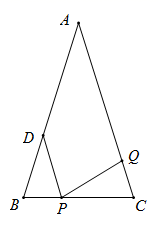

(1)、如果点P在线段BC上以2cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动．
①若点Q的运动速度与点P的运动速度相等，经过2s后，△BPD与△CQP是否全等，请说明理由；

②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？

(2)、若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？

查看试题解析