广东省广州市花都区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-20 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个手机软件图标中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $a^{2} \cdot a^{2} = 2 a^{2}$ C、 $6 a^{5} \div 3 a^{3} = 2 a^{2}$ D、 ${(- a^{2})}^{3} = - a^{5}$

查看试题解析
3. 下列长度的线段能组成三角形的是（）

A、3、4、8 B、5、6、11 C、5、6、10 D、3、5、10

查看试题解析
4. 广州市发布2019年上半年空气质量状况，城区PM2.5平均浓度为0.000029克/立方米，0.000029用科学记数法表示为（）

A、2.9 $\times 10^{- 5}$ B、2.9 $\times 10^{5}$ C、2.9 $\times 10^{- 6}$ D、2.9 $\times 10^{6}$

查看试题解析
5. 如图，若 $△ ABC ≅ △ DEF$ ，BC=7，CF=5，则CE的长为（）

A、1 B、2 C、2.5 D、3

查看试题解析
6. 计算：21 $\times 3.14$ +79 $\times 3.14$ =（）

A、282.6 B、289 C、354.4 D、314

查看试题解析
7. 若 $\times x y = 3 x^{2} y + 2 x y$ ，则内应填的式子是（）

A、 $3 x + 2$ B、 $x + 2$ C、3 $x y + 2$ D、 $x y + 2$

查看试题解析
8. 如图，一副三角板叠在一起，最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上，AC与DE交于点M，如果 $∠ B D F = 105 °$ ，则 $∠ A M D$ 的度数为（）

A、80 $°$ B、85 $°$ C、90 $°$ D、95 $°$

查看试题解析
9. 已知a²+b²＝6ab，且ab≠0，则 $\frac{{(a + b)}^{2}}{a b}$ 的值为（）

A、2 B、4 C、6 D、8

查看试题解析
10. 如图，AD//BC，点E是线段AB的中点，DE平分 $∠ A D C$ ， BC=AD+2，CD=7，则 ${BC}^{2} - {AD}^{2}$ 的值等于（）

A、14 B、9 C、8 D、5

查看试题解析

二、填空题

11. 在平面直角坐标系中，点A（3，-2）关于y轴对称的点坐标为．

查看试题解析
12. 如图，点D、E分别在线段AB、AC上，且AD=AE，若由SAS判定 $△ ABE ≅ △ ACD$ ，则需要添加的一个条件是．

查看试题解析
13. 在△ABC中， $∠ C = 90 °$ ，AB=4， $∠ A = 60 °$ ，则AC= ．

查看试题解析
14. 若分式 $\frac{| x | - 2}{x + 2}$ 的值为0，则 $x$ 的值是．

查看试题解析
15. 已知 $x^{m} = 3, x^{n} = 5$ ,则 $x^{2 m + n}$ 的值为．

查看试题解析
16. 如图，已知 $∠ A = 30 °$ ，AB=BC，点D是射线AE上的一动点，当BD+CD最短时， $∠ A B D$ 的度数是．

查看试题解析

三、解答题

17. 因式分解： $(x + 1) (x + 3) - 3$

查看试题解析
18. 解方程： $\frac{3}{x - 2} = \frac{2}{x}$ ．

查看试题解析
19. 如图，AB=AC， $∠ BAE = ∠ CAD$ ， $∠ D = ∠ E .$ 求证：BD=CE.

查看试题解析
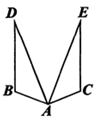20. 如图，在四边形ABCD中， $∠ C + ∠ D = 210 °$ ．

(1)、 ∠DAB+∠CBA=度；

(2)、若 $∠ D A B$ 的角平分线与 $∠ C B A$ 的角平分线相交于点E，求 $∠ E$ 的度数．

查看试题解析
21. 化简并求值： $(\frac{a^{2}}{a - 2} + \frac{1}{2 - a}) \div \frac{a - 1}{a (a - 2)}$ ，其中 $a = 3$

查看试题解析
22. 如图，AB是线段，AD和BC是射线，AD//BC．

(1)、尺规作图：作AB的垂直平分线EF，垂足为O，且分别与射线BC、AD相交于点E、F（不写作法，保留作图痕迹）；

(2)、在（1）条件下，连接AE，求证：AE=AF．

查看试题解析
23. 广州市花都区某校八年级有180名同学参加地震应急演练，对比发现：经专家指导后，平均每秒撤离的人数是专家指导前的3倍，这180名同学全部撤离的时间比专家指导前快2分钟. 求专家指导前平均每秒撤离的人数．

查看试题解析
24. 如图（1），在 $Rt △$ ABC中， $∠ C = 90 °$ ，BC=9cm， AC=12cm， AB=15cm.现有一动点P，从点A出发，沿着三角形的边AC $\to$ CB $\to$ BA运动，回到点A停止，速度为3cm/s，设运动时间为ts．

(1)、如图（1），当t=时，△APC的面积等于△ABC面积的一半；

(2)、如图（2），在△DEF中， $∠ E = 90 °$ ，DE=4cm， DF=5cm， $∠ D = ∠ A$ ．在△ABC的边上，若另外有一个动点Q，与点P同时从点A出发，沿着AB $\to$ BC $\to$ CA运动，回到点A停止．在两点运动过程中的某一时刻，恰好 $△ APQ ≅ △ DEF$ ，求点Q的运动速度．

查看试题解析
25. 在平面直角坐标系中，点A（4，0），B（0，4），点C是x轴负半轴上的一动点，连接BC，过点A作直线BC的垂线，垂足为D，交y轴于点E．

(1)、如图（1），
①判断 $∠ BCO$ 与 $∠ AEO$ 是否相等.

②若OC=2，求点E的坐标．

(2)、如图（2），若OC<4，连接DO，求证：DO平分 $∠ ADC$ ．

(3)、若OC>4时，请问（2）的结论是否成立？若成立，画出图形，并证明；若不成立，说明理由．

查看试题解析