广东省佛山市南海区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-10-20 类型:期末考试
一、单选题
-
1. 在下列各组数据中,不能作为直角三角形三边边长的是( )A、3,3,3 B、3,4,5 C、5,12,13 D、6,8,102. 下列各数中与 相乘结果为有理数的是( )A、 B、 C、2 D、3. 如果点P(m+3,m+1)在x轴上,则点P的坐标为( )A、(0,2) B、(2,0) C、(4,0) D、(0,﹣4)4. 下列各式中,运算正确的是( )A、 B、 C、 D、5. 下列命题为真命题的是( )A、两个锐角之和一定是钝角 B、两直线平行,同旁内角相等 C、如果x2>0,那么x>0 D、平行于同一条直线的两条直线平行6. 二元一次方程组 的解是( )A、 B、 C、 D、7. 下列图象中,以方程y﹣2x﹣2=0的解为坐标的点组成的图象是( )A、
 B、
B、 C、
C、 D、
D、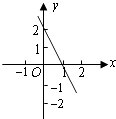 8. 已知 ,则x+y的值为( )A、0 B、﹣1 C、1 D、59. 如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
8. 已知 ,则x+y的值为( )A、0 B、﹣1 C、1 D、59. 如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( ) A、45° B、54° C、40° D、50°10. 有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是( )
A、45° B、54° C、40° D、50°10. 有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是( ) A、1 B、2018 C、2019 D、2020
A、1 B、2018 C、2019 D、2020二、填空题
-
11. 的平方根是;64的立方根是 .12. 某地教育局拟招聘一批数学教师,现有一名应聘者笔试成绩88分、面试成绩90分,综合成绩按照笔试占45%、面试占55%进行计算,该应聘者的综合成绩为分.13. 为了比较 +1与 的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=3,D在BC上且BD=AC=1.通过计算可得 +1 .(填“>”或“<”或“=”)
 14. 一副分别含有30°和45°角的两个直角三角板,拼成如下图形,则∠1= 度.
14. 一副分别含有30°和45°角的两个直角三角板,拼成如下图形,则∠1= 度. 15. 如图,边长为4的等边△AOB在平面直角坐标系中的位置如图所示,则点A的坐标为 .
15. 如图,边长为4的等边△AOB在平面直角坐标系中的位置如图所示,则点A的坐标为 . 16. 如图,三角形ABC中,∠ACB=90°,AC=3,BC=4,AB=5,P为直线AB上一动点,连PC,则线段PC的最小值是 .
16. 如图,三角形ABC中,∠ACB=90°,AC=3,BC=4,AB=5,P为直线AB上一动点,连PC,则线段PC的最小值是 .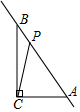 17. 将长为25cm、宽为10cm的长方形白纸,按如下图所示的方法粘合起来,粘合部分的宽为2cm,设x张白纸粘合后的总长度为ycm,y与x的函数关系式为 .
17. 将长为25cm、宽为10cm的长方形白纸,按如下图所示的方法粘合起来,粘合部分的宽为2cm,设x张白纸粘合后的总长度为ycm,y与x的函数关系式为 .
三、解答题
-
18. 计算: -19. 2019国际篮联篮球世界杯的D组小组赛由佛山赛区承办,小李在网上预定了小组赛和淘汰赛两个阶段的球票共10张,总价为3400元,其中小组赛球票每张280元,淘汰赛球票每张580元,问小李预定了小组赛和淘汰赛的球票各多少张?20. 如图,已知CE⊥AB,MN⊥AB,∠1=∠2,求证:∠EDC+∠ACB=180°.
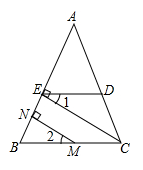 21. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3).
21. 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(-4,5),(-1,3). (1)、请在如图所示的网格平面内作出平面直角坐标系;(2)、请作出△ABC关于y轴对称的△A′B′C′;(3)、写出点B′的坐标.22. 为了减少二氧化碳的排放量,提倡绿色出行,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付(使用的前1小时免费)和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)、请在如图所示的网格平面内作出平面直角坐标系;(2)、请作出△ABC关于y轴对称的△A′B′C′;(3)、写出点B′的坐标.22. 为了减少二氧化碳的排放量,提倡绿色出行,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付(使用的前1小时免费)和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题: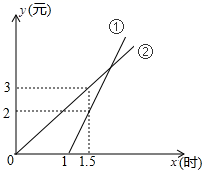 (1)、图中表示会员卡支付的收费方式是(填①或②).(2)、在图①中当x≥1时,求y与x的函数关系式.(3)、陈老师经常骑行该公司的共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.23. 某中学举办“网络安全知识答题竞赛”,七、八年级根据初赛成绩各选出5名选手组成代表队参加决赛,两个队各选出的5名选手的决赛成绩如图所示.
(1)、图中表示会员卡支付的收费方式是(填①或②).(2)、在图①中当x≥1时,求y与x的函数关系式.(3)、陈老师经常骑行该公司的共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.23. 某中学举办“网络安全知识答题竞赛”,七、八年级根据初赛成绩各选出5名选手组成代表队参加决赛,两个队各选出的5名选手的决赛成绩如图所示.平均分(分)
中位数(分)
众数(分)
方差(分2)
七年级
a
85
b
S七年级2
八年级
85
c
100
160
 (1)、根据图示填空:a= , b= , c=;(2)、结合两队成绩的平均数和中位数进行分析,哪个代表队的决赛成绩较好?(3)、计算七年级代表队决赛成绩的方差S七年级2 , 并判断哪一个代表队选手成绩较为稳定.24. 如图,在平面直角坐标系中,直线y=−2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C.
(1)、根据图示填空:a= , b= , c=;(2)、结合两队成绩的平均数和中位数进行分析,哪个代表队的决赛成绩较好?(3)、计算七年级代表队决赛成绩的方差S七年级2 , 并判断哪一个代表队选手成绩较为稳定.24. 如图,在平面直角坐标系中,直线y=−2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C. (1)、求点C的坐标.(2)、若P是x轴上的一个动点,直接写出当△POC是等腰三角形时P的坐标.(3)、在直线AB上是否存在点M,使得△MOC的面积是△AOC面积的2倍?若存在,请求出点M的坐标;若不存在,请说明理由.25. 阅读下面的材料,并解决问题.
(1)、求点C的坐标.(2)、若P是x轴上的一个动点,直接写出当△POC是等腰三角形时P的坐标.(3)、在直线AB上是否存在点M,使得△MOC的面积是△AOC面积的2倍?若存在,请求出点M的坐标;若不存在,请说明理由.25. 阅读下面的材料,并解决问题.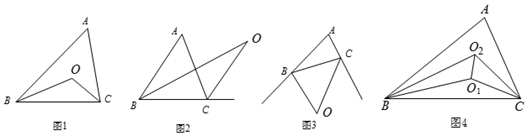
 (1)、已知在△ABC中,∠A=60°,图1-图3的△ABC的内角平分线或外角平分线交于点O,请直接求出下列角度的度数.
(1)、已知在△ABC中,∠A=60°,图1-图3的△ABC的内角平分线或外角平分线交于点O,请直接求出下列角度的度数.如图1,∠O=; 如图2,∠O=; 如图3,∠O=;如图4,∠ABC,∠ACB的三等分线交于点O1 , O2 , 连接O1O2 , 则∠BO2O1= .
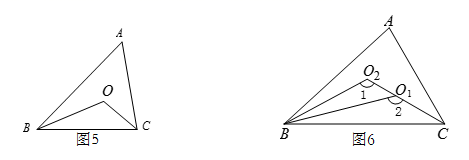
(2)、如图5,点O是△ABC两条内角平分线的交点,求证:∠O=90°+ ∠A.(3)、如图6,△ABC中,∠ABC的三等分线分别与∠ACB的平分线交于点O1 , O2 , 若∠1=115°,∠2=135°,求∠A的度数.