广东省佛山市禅城区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-10-20 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点（﹣8，2）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下面各组数中不能构成直角三角形三边长的一组数是（）

A、3、4、5 B、6、8、10 C、5、12、13 D、11、12、15

查看试题解析
3. 下列各组数值是二元一次方程x﹣3y＝4的解的是（）

A、 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ C、 ${\begin{array}{l} x = - 1 \\ y = - 2 \end{array}$ D、 ${\begin{array}{l} x = 4 \\ y = - 1 \end{array}$

查看试题解析
4. 下列实数是无理数的是（）

A、 $- 2020$ B、 $\sqrt{2}$ C、 $3.14159$ D、 $\frac{1}{6}$

查看试题解析
5. 实数 $\sqrt{38}$ 的值在（）

A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间

查看试题解析
6. 下列语句不是命题的是（）

A、连结AB B、对顶角相等 C、相等的角是对顶角 D、同角的余角相等

查看试题解析
7. 等腰三角形的两边长分别为3cm和7cm，则周长为（　　）

A、13cm B、17cm C、13cm或17cm D、11cm或17cm

查看试题解析
8. 解方程组 ${\begin{array}{l} 2 a + b = 7 ① \\ a - b = 2 ② \end{array}$ 的最佳方法是（）

A、代入法消去a,由②得 $a = b + 2$ B、代入法消去b,由①得 $b = 7 - 2 a$ C、加减法消去a,①-②×2得 $3 b = 3$ D、加减法消去b,①+②得 $3 a = 9$

查看试题解析

9. 如表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差：

	甲	乙	丙	丁
平均数 $\bar{x}$ （厘米）	$375$	$350$	$375$	$350$
方差 $s^{2}$	$12.5$	$13.5$	$2.4$	$5.4$

要从中选择一名成绩好又发挥稳定的运动员参加决赛，最合适的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

10. 如图，围棋棋盘放在某平面直角坐标系内，已知黑棋(甲)的坐标为(﹣2，2)黑棋(乙)的坐标为(﹣1，﹣2)，则白棋(甲)的坐标是（）

A、(2，2) B、(0，1) C、(2，﹣1) D、(2，1)

查看试题解析

二、填空题

11. 16的平方根是，9的立方根是．

查看试题解析
12. 如图，已知∠1＝∠2，∠B＝35°，则∠3＝°.

查看试题解析
13. 计算 $\frac{\sqrt{3} \times \sqrt{12}}{\sqrt{2}}$ 的结果是．

查看试题解析
14. 如图，一座城墙高11.7米，墙外有一个宽为9米的护城河，那么一个长为15米的云梯（填“能”或“否”）到达墙的顶端．

查看试题解析
15. 如图，已知直线y＝ax+b和直线y＝kx交于点P，则关于x，y的二元一次方程组 ${\begin{array}{l} y = k x \\ y = a x + b \end{array}$ 的解是．

查看试题解析
16. 如图，在平面直角坐标系中，对 $Δ A B C$ 进行循环往复的轴对称变换，若原来点 $A$ 坐标是 $(a ， b)$ ，则经过第2016变换后所得的 $A$ 点坐标是．

查看试题解析
17. 如图，直线 $y = \frac{4}{3} x + 4$ 交x轴于点A，交y轴于点B，点C为线段OB上一点，将 $△ ABC$ 沿着直线AC翻折，点B恰好落在x轴上的D处，则 $△ ACD$ 的面积为．

查看试题解析

三、解答题

18. 计算：

(1)、 $\sqrt{20} - \sqrt{5} + 3 \sqrt{\frac{1}{5}}$

(2)、 $(\sqrt{6} - \sqrt{3}) \times \sqrt{12}$

查看试题解析
19. 解方程组： ${\begin{matrix} 4 x - 3 y = 1 ① \\ x - 2 y = 4 ② \end{matrix}$ .

查看试题解析
20. 如图，在平面直角坐标系中，点 $O$ 为坐标原点，已知 $Δ A B C$ 三个定点坐标分别为 $A (- 4 ， 1)$ ， $B (- 3 ， 3)$ ， $C (- 1 ， 2)$ .

(1)、画出 $Δ A B C$ 关于 $x$ 轴对称的 $Δ A_{1} B_{1} C_{1}$ ，点 $A ， B ， C$ 的对称点分别是点 $A_{1} 、 B_{1} 、 C_{1}$ ，则 $A_{1} 、 B_{1} 、 C_{1}$ 的坐标： $A_{1}$ （，）， $B_{1}$ （，）， $C_{1}$ （，）；

(2)、画出点 $C$ 关于 $y$ 轴的对称点 $C_{2}$ ，连接 $C_{1} C_{2}$ ， $C C_{2}$ ， $C_{1} C$ ，则 $Δ C C_{1} C_{2}$ 的面积是.

查看试题解析
21. 某校在八年级开展环保知识问卷调查活动，问卷一共10道题，八年级（三）班的问卷得分情况统计图如下图所示：

(1)、扇形统计图中，a=；

(2)、根据以上统计图中的信息，
①问卷得分的极差是分；②问卷得分的众数是分；③问卷得分的中位数是分；

(3)、请你求出该班同学的平均分.

查看试题解析
22. 一个零件的形状如图所示，工人师傅按规定做得∠B=90°，
AB＝3，BC＝4，CD＝12，AD＝13，假如这是一块钢板，你能帮工人师傅计算一下这块钢板的面积吗？

查看试题解析
23. 探究问题：已知 $∠ A B C$ ，画一个角 $∠ D E F$ ，使 $D E / / A B ， E F / / B C$ ，且 $D E$ 交 $B C$ 于点 $P$ . $∠ A B C$ 与 $∠ D E F$ 有怎样的数量关系？

(1)、我们发现 $∠ A B C$ 与 $∠ D E F$ 有两种位置关系：如图1与图2所示.
①图1中 $∠ A B C$ 与 $∠ D E F$ 数量关系为；图2中 $∠ A B C$ 与 $∠ D E F$ 数量关系为.请选择其中一种情况说明理由.

②由①得出一个真命题（用文字叙述）：.

(2)、应用②中的真命题，解决以下问题：若两个角的两边互相平行，且一个角比另一个角的2倍少30°，请直接写出这两个角的度数.

查看试题解析
24. 甲、乙两车分别从A、B两地同时出发，在同一条公路上，匀速行驶，相向而行，到两车相遇时停止.甲车行驶一段时间后，因故停车0.5小时，故障解除后，继续以原速向B地行驶，两车之间的路程y（千米）与出发后所用时间x(小时）之间的函数关系如图所示.

(1)、求甲、乙两车行驶的速度V_甲、V_乙.

(2)、求m的值.

(3)、若甲车没有故障停车，求可以提前多长时间两车相遇.

查看试题解析
25. 如图，在平面直角坐标系中，直线l₁的解析式为y=x，直线l₂的解析式为 $y = - \frac{1}{2} x + 3$ ，与x轴、y轴分别交于点A、点B，直线l₁与l₂交于点C．

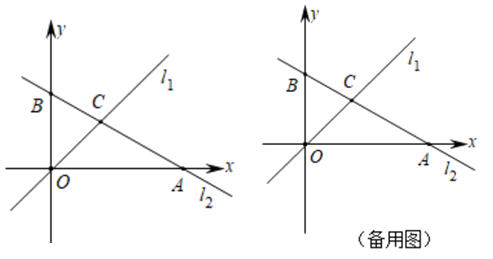(1)、求点A、点B、点C的坐标，并求出△COB的面积；

(2)、若直线l₂上存在点P(不与B重合)，满足S_△COP=S_△COB ，请求出点P的坐标；

(3)、在y轴右侧有一动直线平行于y轴，分别与l₁ ， l₂交于点M、N，且点M在点N的下方，y轴上是否存在点Q，使△MNQ为等腰直角三角形?若存在，请直接写出满足条件的点Q的坐标；若不存在，请说明理由．

查看试题解析