初中数学浙教版七年级上学期期中复习专题3 实数的认识与大小比较

试卷更新日期：2020-10-20 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列各个数中比-2小的数（）

A、-3 B、0 C、5 D、-1

查看试题解析
2. 下列说法正确的是（）

A、0不是正数，不是负数，也不是整数 B、正整数与负整数包括所有的整数 C、–0.6是分数，负数，也是有理数 D、没有最小的有理数，也没有最小的自然数

查看试题解析
3. 下列说法正确的是（）.

A、若两个数的绝对值相等，则这两个数必相等 B、若两数不相等，则这两数的绝对值一定不相等 C、若两数相等，则这两数的绝对值相等 D、两数比较大小，绝对值大的数大

查看试题解析
4. 在实数 $- \sqrt{2}$ ，-1，0，1中，最小的是（）

A、 $- \sqrt{2}$ B、-1 C、0 D、1

查看试题解析
5. 估计 $\sqrt{22}$ 的值在（）

A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间

查看试题解析
6. 下列各数中，比3大比4小的无理数是（）

A、3.14 B、 $\frac{10}{3}$ C、 $\sqrt{12}$ D、 $\sqrt{17}$

查看试题解析
7. 已知a，b，c三个数在数轴上的位置如图所示，则下列各式中正确的个数为（）

①ab > 0 ②b - c > 0 ③|b - c| > c - b ④ $\frac{1}{a}$ > $\frac{1}{b}$ ⑤ $\frac{1}{b}$ > $\frac{1}{c}$

A、4个 B、3个 C、2个 D、1个

查看试题解析
8. 在实数 $\frac{22}{7}$ ， $\sqrt{7}$ ， $\sqrt[3]{9}$ ， $\sqrt{36}$ ， $\frac{π}{3}$ 中，无理数有（）.

A、2个 B、3个 C、4个 D、5个

查看试题解析
9. 如图，M、N、P、Q是数轴上的四个点，这四个点中最适合表示 $\sqrt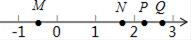{15}$ ﹣1的点是（　　）

A、点M B、点N C、点P D、点Q

查看试题解析
10. 某测绘小组的技术员要测量A，B两处的高度差（A，B两处无法直接测量），他们首先选择了D，E，F，G四个中间点，并测得它们的高度差如下表：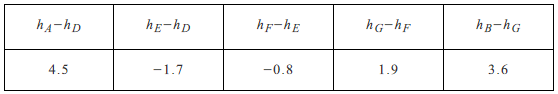

根据以上数据，可以判断A，B之间的高度关系为（）

A、B处比A处高 B、A处比B处高 C、A，B两处一样高 D、无法确定

查看试题解析

二、填空题

11. 比较大小：－3 $- \frac{1}{2}$ （填“＞” 或“＜”）

查看试题解析
12. 若m＜2 ＜m+1，且m为整数，则m＝.

查看试题解析
13. 比较大小： $3 \sqrt{2}$ $2 \sqrt{3}$ （填“＞”或“＜”＝）.

查看试题解析
14. 在数轴上A表示– $\frac{5}{6}$ ，点B表示 $\frac{3}{4}$ ，则点离原点的距离近些.

查看试题解析
15. 已知如下各数：4， $- \frac{3}{2}$ ，0，-4，2.5，-1，解答下列各题

(1)、用“＞”号把这些数连接起来

(2)、这些数的绝对值的和是

查看试题解析
16. 已知a＞0，b＜0，|b|＞|a|，比较a ， ﹣a ， b ， ﹣b四个数的大小关系，用“＜”把它们连接起来．

查看试题解析
17. 已知点O为数轴的原点，点A ， B在数轴上若AO＝8，AB＝2，且点A表示的数比点B表示的数小，则点B表示的数是．

查看试题解析
18. 如图，以原点O为圆心， $O B$ 为半径画弧与数轴交于点A，则点A在数轴上表示的数为.

查看试题解析

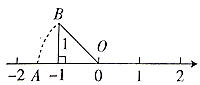
三、解答题

19. 在数轴上表示下列各数，并把这些数按从小到大的顺序用“＜”连接.
-（-1.5），3， $- \sqrt{2.25}$ ，|- 4|

查看试题解析
20. 阅读材料：
图中是小马同学的作业，老师看了后，找来小马问道：“小马同学，你标在数轴上的两个点对应题中的两个无理数，是吗？”

小马点点头.

老师又说：“你这两个无理数对应的点找的非常准确，遗憾的是没有完成全部解答.”

请你帮小马同学完成本次作业.

请把实数0，﹣π，﹣2， $\sqrt{8}$ ，1表示在数轴上，并比较它们的大小（用＜号连接）.

解：

查看试题解析
21. 已知a是 $\sqrt{10}$ 的整数部分，b是它的小数部分，求(－a)³＋(b＋3)²的值.

查看试题解析
22. 已知2a－1的平方根是±3，3a＋b－9的立方根是2，c是 $\sqrt{8}$ 的整数部分，求a＋b＋c的平方根．

查看试题解析
23. 已知有理数a，b，c在数轴上的位置如图所示.

(1)、分别判断a，b，c，a+b的正负；

(2)、用符号“<”连接下列各数：a，b，c，－a，－b.

查看试题解析
24. 问题：你能比较两个数 2018²⁰¹⁹与2019²⁰¹⁸的大小吗？为了解决这个问题，我们先把它抽象成这样的问题：写成它的一般形式，即比较nⁿ⁺¹和（n+1）ⁿ的大小（n是非零自然数）．然后，我们分析n=1，n=2，n=3…这些简单情形入手，从而发现规律，经过归纳，猜想出结论．

(1)、通过计算，比较下列各组中两个数的大小
①1² 2¹② 2³ 3²③ 3⁴ 4³④ 4⁵ 5⁴⑤5⁶ 6⁵⑥ 6⁷ 7⁶

(2)、从第（1）题的结果经过归纳，可以猜想nⁿ⁺¹和（n+1）ⁿ的大小关系；

(3)、根据上面归纳猜想得到的一般结论，试比较下列两个数的大小：2018²⁰¹⁹ 2019²⁰¹⁸ ．

查看试题解析
25. 已知 a、b、c 在数轴上的位置如图：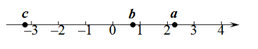

(1)、用“<”或“>”填空：a+10； c-b0； b-10；

(2)、化简： $| a + 1 | - | c - b | - | b - 1 |$ ；

(3)、若a+b+c=0，且b与-1的距离和c与-1的距离相等，求下列式子的值：2b -c - (a - 4c - b)．

查看试题解析
26. 阅读下列信息材料
信息1：因为无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来，比如、 $π$ 、 $\sqrt{2}$ 等，而常用的“……”或者“ $\approx$ ”的表示方法都不够百分百准确；

信息2： $2.5$ 的小数部分是0.5，可以看成 $2.5 - 2$ 得来的：

信息3：任何一个无理数，都可以夹在两个相邻的整数之间，如 $2 < \sqrt{5} < 3$ ，是因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ：

根据上述信息，回答下列问题：

(1)、若 $21 < a < 22$ ，则a的小数部分可以表示为；

(2)、 $10 + \sqrt{3}$ 也是夹在两个整数之间的，可以表示为 $a < 10 + \sqrt{3} < b$ 则 $a + b =$ ；

(3)、若 $\sqrt{30} - 3 = x + y$ ，其中x是整数，且 $0 < y < 1$ ，请求x-y的相反数．

查看试题解析