初中数学北师大版八年级上学期 第五章 5.7用二元一次方程组确定函数表达式

试卷更新日期：2020-10-20 类型：同步测试

进入 出卷网 下载

一、单选题

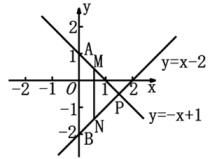
  • 1. 如图直线y1=k1x-b与直线y2=k2x相交于点P(1，-2)，则方程组 {y=k2xy=−k1x−b 的解是（ ）

    A、{x=−1y=2 B、{x=−1y=−2 C、{x=1y=2 D、{x=1y=−2    

    查看试题解析

  • 2. 如图，过点A的一次函数的图象与正比例函数y=2x的图象相交于点B，能表示这个一次函数图象的方程是（  ）

    A、2x−y+3=O B、x−y−3=0 C、2y−x+3=0 D、x+y−3=0

    查看试题解析

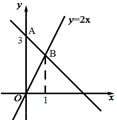  • 3. 直线y=2x－4与y=－x+2的公共点坐标为（ ）
    A、(－2，0) B、(0，－2) C、(2，0) D、(0，2)

    查看试题解析

  • 4. 已知直线y＝－x＋4与y＝x＋2如图所示，则方程组 {y=−x+4y=x+2 的解为（ ）

    A、{x=3y=1 B、{x=1y=3 C、{x=0y=4 D、{x=4y=0

    查看试题解析

二、填空题

  • 5. 如图，利用函数图象回答下列问题：方程组 {x+y=3y=2x 的解为 ．

    查看试题解析

  • 6. 已知方程组 {y−ax=cy−kx=b （a、b、c、k为常数， ak≠0 ）的解为 {x=−2y=3 ，则直线 y=ax+c 和直线 y=kx+b 的交点坐标为.

    查看试题解析

  • 7. 如图，已知函数y＝ax+b和y＝kx的图象交于点P，则根据图象可得，关于x，y的二元一次方程组 {y=ax+by=kx 的解是 ．

    查看试题解析

三、综合题

  • 8. 已知直线 2x+y=3 与直线 x−y=3 相交于点A，点 B(a,0) 在 x 轴的正半轴上，且 OB≤OA ．
    (1)、求点A坐标；
    (2)、求 ΔAOB 的面积S与 a 的函数关系式，并求S的取值范围．

    查看试题解析

  • 9. 某服装店销售10套A品牌运动装和20套B品脾运动装的利润为4000元，销售20套A品牌运动装和10套B品牌运动装的利润为3500元。
    (1)、该服装店计划一次购进两种品牌的运动装共100套，设服装店购进A品牌运动装x套，这100套运动装的销售总利润为y元，求y关于x的函数关系式；
    (2)、在(1)的条件下，若B品牌运动装的进货量不超过A品牌的2倍，该服装店购进A、B两种品牌运动装各多少套，才能使销售总利润最大?
    (3)、实际进货时，厂家对A品牌运动装出厂价下调，且限定超市最多购进A品牌运动装70套，A品牌运动装的进价降低了m(0<m<100)元，若服装店保持两种运动装的售价不变，请你根据以上信息及(2)中的条件，设计出使这100套运动装销售总利润最大的进货方案。

    查看试题解析

  • 10. 某经销商从市场得知如下信息：

    A品牌手机

    B品牌手机

    进价（元/部）

    700

    100

    售价（元/部）

    900

    160

    他计划用4万元资金一次性购进这两种品牌手机共100部，设该经销商购进A品牌手机X部，这两种品牌手机全部销售完后获得利润为y元。

    (1)、试写出y与x之间的函数关系式：


    (2)、若要求全部销售完后获得的利润不少于1.26万元，该经销商有哪几种进货方案？


    (3)、选择哪种进货方案，该经销商可获利最大？最大利润是多少元？


    查看试题解析

  • 11. 如图，直线l1：y=2x-3与x轴交于点D，直线l2：y=kx+b经过点B(3，1)，且与直线l1交于点C(m，2)。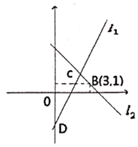

    (1)、求点D的坐标：
    (2)、求直线l2的解析式：
    (3)、利用函数图象写出关于x，y的二元一次方程组 {y=2x−3y=kx+b 的解。

    查看试题解析

  • 12. 如图，直线y=-x+1和直线y=x-2相交于点P，分别与y轴交于A、B两点．

    (1)、求点P的坐标；
    (2)、求△ABP的面积；
    (3)、M、N分别是直线y=-x+1和y=x-2上的两个动点，且MN∥y轴，若MN=5，直接写出M、N两点的坐标．

    查看试题解析

  • 13. 如图，直线l1过点A（8，0）、B（0，﹣5），直线l2过点C（0，﹣1），l1、l2相交于点D，且△DCB的面积等于8.

    (1)、求点D的坐标；
    (2)、点D的坐标是哪个二元一次方程组的解.

    查看试题解析