初中数学北师大版八年级上学期 第五章 5.6二元一次方程与一次函数
试卷更新日期:2020-10-20 类型:同步测试
一、单选题
-
1. 如图,以两条直线l1 , l2的交点坐标为解的方程组是( )
 A、 B、 C、 D、2. 在同一直角坐标系内,若直线y=2x-1与直线y=-2x+m的交点在第四象限,则m的取值范围是( )A、m>—1 B、m<1 C、—1<m<1 D、—1≤m≤13. 已知一次函数 和一次函数 的图象的交点坐标是 ,据此可知方程组 的解为( )A、 B、 C、 D、4. 已知二元一次方程组 的解为 ,则在同一平面直角坐标系中,两函数y=x+5与y=﹣ x﹣1的图像的交点坐标为( )A、(﹣4,1) B、(1,﹣4) C、(4,﹣1) D、(﹣1,4)
A、 B、 C、 D、2. 在同一直角坐标系内,若直线y=2x-1与直线y=-2x+m的交点在第四象限,则m的取值范围是( )A、m>—1 B、m<1 C、—1<m<1 D、—1≤m≤13. 已知一次函数 和一次函数 的图象的交点坐标是 ,据此可知方程组 的解为( )A、 B、 C、 D、4. 已知二元一次方程组 的解为 ,则在同一平面直角坐标系中,两函数y=x+5与y=﹣ x﹣1的图像的交点坐标为( )A、(﹣4,1) B、(1,﹣4) C、(4,﹣1) D、(﹣1,4)二、填空题
-
5. 若一次函数y=3x-5的图像l1与y=2x+1的图像l2相交于点P,则点P的坐标是( , )。6. 画出函数y1=-x+1,y2=2x-5 的图象,利用图象回答下列问题:
 (1)、方程组 的解是 .(2)、y1随x增大而 , y2随x增大而 .(3)、当y1>y2时,x的取值范围 是 .7. 已知直线y=x-3与y=2x+2的交点为(-5,-8),则方程组 的解是 .8. 如图,已知一次函数y=kx+3和y=-x+b的图象交于点P (2,4).则关于x的方程kx+3=-x+b 的解是 .
(1)、方程组 的解是 .(2)、y1随x增大而 , y2随x增大而 .(3)、当y1>y2时,x的取值范围 是 .7. 已知直线y=x-3与y=2x+2的交点为(-5,-8),则方程组 的解是 .8. 如图,已知一次函数y=kx+3和y=-x+b的图象交于点P (2,4).则关于x的方程kx+3=-x+b 的解是 .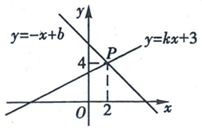 9. 如图,直线 与直线 相交于点 ,则方程组 的解是.
9. 如图,直线 与直线 相交于点 ,则方程组 的解是.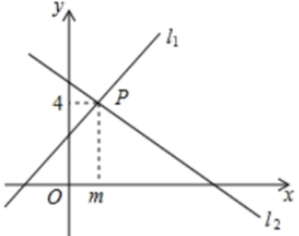
三、综合题
-
10. 为了抗击新冠疫情,我市甲乙两厂积极生产了某种防疫物资共500吨,乙厂的生产量是甲厂的2倍少100吨,这批防疫物资将运往A地240吨,B地260吨,运费如下:(单位:吨)
A B 甲 20 25 乙 15 24 (1)、求甲乙两厂各生产了这批防疫多少吨?(2)、设这批物资从乙厂运往A地x吨,全部运往A,B两地的总运费为y元,求y与x之间的函数关系式,并设计使总运费最少的调运方案;(3)、当每吨运费降低m元,( 且m为整数),按(2)中设计的调运方案运输,总运费不超过5200元,求m的最小值.11. 学校为奖励在家自主学习有突出表现的学生,决定购买笔记本和钢笔作为奖品。已知1本笔记本和4支钢笔共需100元,4本笔记本和6支钢笔共需190元。(1)、分别求一本笔记本和一支钢笔的售价;(2)、若学校准备购进这两种奖品共90份,并且笔记本的数量不多于钢笔数量的3倍,请设计出最省钱的购买方案,并说明理由。12. 下表是小丽在某路口统计20分钟各种车辆通过情况的记录表,其中空格处的字迹已模糊。电瓶车
公交车
货车
小轿车
合计(车流总量)
(第一时段)8:50~9:00
m
86
161
(第二时段)9:00~9:10
7n
m
n
99
合计
30
185
(1)、根据表格信息,在表格中填写第一时段电瓶车和货车的数量。(2)、在第二时段内,电瓶车和公交车的车辆数之和恰好是第二时段车流总量的一半,且两个时段的电瓶车总数为170辆。①求m,n的值。
②因为第二时段内车流总量较多,造成了交通拥堵现象,据估计,该时段内,每增加1辆公交车,可减少8辆小轿车和5辆电瓶年,若要使得第二时段和第一时段的车流总量最接近,则应增加几辆公交车?
13. 在创建全国文明城市过程中,官渡区决定购买A、B两种树苗对某路段道路进行绿化改造.已知购买A种树苗5棵,B种树苗3棵,需要840元;购买A种树苗3棵,B种树苗5棵,需要760元.(1)、求购买A、B两种树苗每棵各需多少元?(2)、现需购进这两种树苗共100棵,考虑到绿化效果和资金周转,购进A种树苗不能少于30棵,且用于购买这两种树苗的资金不能超过10000元,怎样购买所需资金最少?