海南省海口九中海甸分校2019-2020学年八年级上学期数学期中考试试卷

试卷更新日期：2020-10-19 类型：期中考试

进入出卷网下载

一、选择题

1. 64的立方根是（　　）

A、4 B、±4 C、8 D、±8

查看试题解析
2. 下列算式中错误的是 $($ $)$

A、 $- \sqrt{0.64} = - 0.8$ B、 $\pm \sqrt{1.96} = \pm 1.4$ C、 $\sqrt{\frac{9}{25}} = \pm \frac{3}{5}$ D、 $^{3} \sqrt{- \frac{27}{8}} = - \frac{3}{2}$

查看试题解析
3. 下列实数中，属于无理数的是（）

A、 $- \frac{4}{7}$ B、0 C、 $\frac{\sqrt{12}}{3}$ D、0.3131131113

查看试题解析
4. 如图，数轴上点P表示的数可能是（）.

A、 $\sqrt{10}$ B、 $\sqrt{5}$ C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看试题解析
5. 若a^m＝2，aⁿ＝3，a^p＝5，则a^2m^＋n－p的值是（ )

A、2.4 B、2 C、1 D、0

查看试题解析
6. 若 $x^{2} + m x + 16$ 能写成另一个整式的平方形式，则 $m$ 的值等于（）

A、4 B、－8 C、8 D、8或－8

查看试题解析
7. 下列从左边到右边的变形，是因式分解的是（）

A、(3－x)(3＋x)＝9－x² B、(y＋1)(y－3)＝－(3－y)(y＋1) C、4yz－2y²z＋z＝2y(2z－yz)＋z D、－8x²＋8x－2＝－2(2x－1)²

查看试题解析
8. 下列各式中，能用完全平方公式分解的个数为（）
① $x^{2} - 10 x + 25$ ；② $4 a^{2} + 4 a - 1$ ；③ $x^{2} - 2 x - 1$ ；④ $- m^{2} + m - \frac{1}{4}$ ；⑤ $4 x^{4} - x^{2} + \frac{1}{4}$ .

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 若n为大于0的整数，则(2n+1)²-(2n-1)²一定是（）

A、6的倍数 B、8的倍数 C、12的倍数 D、16的倍数

查看试题解析
10. 下列句子是命题的有（）
①一个角的补角比这个角的余角大多少度？

②垂线段最短，对吗？

③等角的补角相等；

④两条直线相交只有一个交点；

⑤同旁内角互补.

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 如图所示，AB∥EF∥CD，∠ABC＝90°，AB＝DC，那么图中的全等三角形有（）

A、3对 B、2对 C、1对 D、0对

查看试题解析
12. 如图，在△ABC中，AC＝5，F是高AD和BE的交点，AD＝BD，则BF的长是（）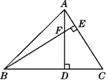

A、7 B、6 C、5 D、4

查看试题解析
13. 如图，在下列条件中，不能证明△ABD≌△ACD的是（）.

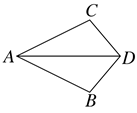A、BD=DC，AB=AC B、∠ADB=∠ADC，BD=DC C、∠B=∠C，∠BAD=∠CAD D、∠B=∠C，BD=DC

查看试题解析
14. 图①是一个边长为 $(m + n)$ 的正方形，小颖将图①中的阴影部分拼成图②的形状，由图①和图②能验证的式子是（）

A、 ${(m + n)}^{2} - {(m - n)}^{2} = 4 m n$ B、 ${(m + n)}^{2} - (m^{2} + n^{2}) = 2 m n$ C、 ${(m - n)}^{2} + 2 m n = m^{2} + n^{2}$ D、 $(m + n) (m - n) = m^{2} - n^{2}$

查看试题解析

二、填空题

15. 计算：(2a)³·(－3a²)＝．

查看试题解析
16. 已知 $x + y = 5$ ， $x - y = 1$ .则代数式 $x^{2} - y^{2}$ 的值是.

查看试题解析
17. 如图，∠A＝∠D＝90°，AC＝DB，欲使OB＝OC，可以先利用“HL”说明Rt_△≌Rt_△得到AB＝DC，再利用证明△AOB≌△DOC得到OB＝OC.

查看试题解析
18. 如图，已知PA⊥ON于A，PB⊥OM于B，且PA=PB，∠MON=50°，∠OPC=30°，则∠PCA=.

查看试题解析

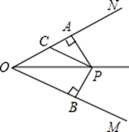
三、解答题

19. 先化简，再求值：(x＋y)(x－y)＋(4xy³－8x²y²)÷4xy，其中x＝1，y＝ $\frac{1}{2}$ .

查看试题解析
20. 计算：

(1)、 $\sqrt{\frac{1}{81}} + \sqrt[3]{- 27} + \sqrt{{(- 2)}^{2}} + {(- 1)}^{2014}$

(2)、(2x- y)²- (2x- y)(2x+y)；

(3)、(x＋5)(x－1)＋(x－2)²

(4)、2013²-2014×2012（用简便方法计算）

查看试题解析
21. 把下列多项式分解因式：

(1)、 $- 2 a^{2} b^{3} + 12 a^{3} b^{2}$

(2)、2x²y－8xy＋8y；

(3)、a²(x－y)＋b²(y－x);

查看试题解析
22. 如图，点E，F在BC上，BE＝CF，∠B＝∠C，AF与DE交于点O.

(1)、请你只添加一个条件，使△ABF≌△DCE，你添加的条件是；

(2)、添加条件后，证明△ABF≌△DCE.

查看试题解析
23.
如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC．

(1)、求证：△ABE≌△CBD；

(2)、若∠CAE=30°，求∠BDC的度数．

查看试题解析