贵州省遵义市湄潭县2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2020-10-19 类型:期中考试
一、选择题
-
1. 如图,射线AB交CD于O,AC=AD,BC=BD,则图中全等三角形的对数是( )
 A、1 B、2 C、3 D、42. 等腰三角形的一个内角是 ,它的底角的大小为( )A、 B、 C、 或 D、 或3. 如图所示,一个60o角的三角形纸片,剪去这个600角后,得到 一个四边形,则么
A、1 B、2 C、3 D、42. 等腰三角形的一个内角是 ,它的底角的大小为( )A、 B、 C、 或 D、 或3. 如图所示,一个60o角的三角形纸片,剪去这个600角后,得到 一个四边形,则么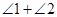 的度数为( )
的度数为( )  A、120O B、180O. C、240O D、30004. 在△ABC内取一点P使得点P到△ABC的三边距离相等,则点P应是△ABC的哪三条线交点 ( )A、高 B、角平分线 C、中线 D、垂直平分线5. 在△ABC与△DEF中,下列六个条件中:①AB=DE;②BC=EF;③AC=DF;④∠A=∠D;⑤∠B=∠E;⑥∠C=∠F,不能判断△ABC与△DEF全等的是( )A、①②④ B、①②③ C、④⑥① D、②③⑥6. 一个正多边形的一个外角是30°,则这个正多边形的对称轴有( )A、9条 B、10条 C、11条 D、12条7. 从一个多边形的一个顶点出发可以引5条对角线,则这个多边形的内角和为( )A、900° B、1080° C、1260° D、1440°8. 下列4个时刻中,是轴对称图形的有( )
A、120O B、180O. C、240O D、30004. 在△ABC内取一点P使得点P到△ABC的三边距离相等,则点P应是△ABC的哪三条线交点 ( )A、高 B、角平分线 C、中线 D、垂直平分线5. 在△ABC与△DEF中,下列六个条件中:①AB=DE;②BC=EF;③AC=DF;④∠A=∠D;⑤∠B=∠E;⑥∠C=∠F,不能判断△ABC与△DEF全等的是( )A、①②④ B、①②③ C、④⑥① D、②③⑥6. 一个正多边形的一个外角是30°,则这个正多边形的对称轴有( )A、9条 B、10条 C、11条 D、12条7. 从一个多边形的一个顶点出发可以引5条对角线,则这个多边形的内角和为( )A、900° B、1080° C、1260° D、1440°8. 下列4个时刻中,是轴对称图形的有( ) A、3个 B、2个 C、1个 D、0个9. 如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )
A、3个 B、2个 C、1个 D、0个9. 如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( )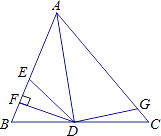 A、11 B、5.5 C、7 D、3.510. 如图, , , 点在 的垂直平分线上,若 ,则 =( )
A、11 B、5.5 C、7 D、3.510. 如图, , , 点在 的垂直平分线上,若 ,则 =( )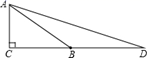 A、4 B、6 C、8 D、1011. 如图,点D是等边△ABC的边AC上一点,以BD为边作等边△BDE,点C,E在BD同侧,下列结论:①∠ABD=30°;②CE∥AB;③CB平分∠ACE;④CE=AD,其中错误的有( )
A、4 B、6 C、8 D、1011. 如图,点D是等边△ABC的边AC上一点,以BD为边作等边△BDE,点C,E在BD同侧,下列结论:①∠ABD=30°;②CE∥AB;③CB平分∠ACE;④CE=AD,其中错误的有( ) A、0个 B、1个 C、2个 D、3个12. 如图,CD是△ABC的角平分线,△ABC的面积为12,BC长为6,点E,F分别是CD,AC上的动点,则AE+EF的最小值是( )
A、0个 B、1个 C、2个 D、3个12. 如图,CD是△ABC的角平分线,△ABC的面积为12,BC长为6,点E,F分别是CD,AC上的动点,则AE+EF的最小值是( ) A、6 B、4 C、3 D、2
A、6 B、4 C、3 D、2二、填空题
-
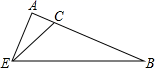
13. 已知:△ABC≌△A′B′C′,∠A=∠A′,∠B=∠B′,∠C=70°,则∠C′=.14. 已知点A(a,b)与点B(﹣5,3)关于x轴对称,则(a﹣b)3=.15. 如图,△ABC的两条高AD,BE交于点F,∠DBF=28°,则∠CAD的度数为.
 16. 如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第10个图形需要黑色棋子的个数是.
16. 如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第10个图形需要黑色棋子的个数是.
三、解答题
-
17. 如图,AD是△ABC中BC边上的高,∠B=∠CAD,求∠BAC的度数.
 18. 如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2).
18. 如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2). (1)、若点D与点A关于y轴对称,则点D的坐标为.(2)、将点B先向右平移5个单位再向上平移1个单位得到点C,则点C的坐标为;(3)、在图上作出点C,D,并顺次连接成四边形ABCD;(4)、四边形ABCD的面积为.19. 如图,△ABC中,BO平分∠ABC,CO平分∠ACB,MN过点O交AB于点M,交AC于点N,且MN∥BC,BM=6,CN=7.求MN的长.
(1)、若点D与点A关于y轴对称,则点D的坐标为.(2)、将点B先向右平移5个单位再向上平移1个单位得到点C,则点C的坐标为;(3)、在图上作出点C,D,并顺次连接成四边形ABCD;(4)、四边形ABCD的面积为.19. 如图,△ABC中,BO平分∠ABC,CO平分∠ACB,MN过点O交AB于点M,交AC于点N,且MN∥BC,BM=6,CN=7.求MN的长. 20. 如图,点E,F在AC上,AE=CF,DF∥BE,且DF=BE.求证:AD∥CB.
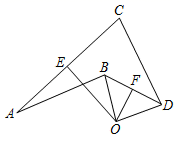
20. 如图,点E,F在AC上,AE=CF,DF∥BE,且DF=BE.求证:AD∥CB. 21. 如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,且AB=CD,∠ABD=120°,∠CDB=38°,求∠OBD的度数.
21. 如图,OE,OF分别是AC,BD的垂直平分线,垂足分别为E,F,且AB=CD,∠ABD=120°,∠CDB=38°,求∠OBD的度数.