云南省昆明市2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-10-19 类型:期末考试
一、填空题
-
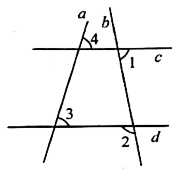
1. 3的算术平方根是 .2. 如图, , ,则 .
 3. “ 的 倍与 的差不小于 ”用不等式表示为.4. 某学校为了了解学生吃早点的情况,选择全校40个班级中学号是5,10,15,20,25,30,35,40的320名同学进行调查,本次调查的样本容量是.5. 某校园一角有如图所示的池塘,为了方便师生游览,现计划从池塘边的点 处搭建一座小桥到甬路边沿 ,请在图中画出小桥距离最短的路径,并测量出小桥在图上的长度为 (精确到小数点后一位).
3. “ 的 倍与 的差不小于 ”用不等式表示为.4. 某学校为了了解学生吃早点的情况,选择全校40个班级中学号是5,10,15,20,25,30,35,40的320名同学进行调查,本次调查的样本容量是.5. 某校园一角有如图所示的池塘,为了方便师生游览,现计划从池塘边的点 处搭建一座小桥到甬路边沿 ,请在图中画出小桥距离最短的路径,并测量出小桥在图上的长度为 (精确到小数点后一位). 6. 如图,在平面直角坐标系 中,点 在 轴上,点 在 轴上,且横坐标为 ,则点 的坐标为.
6. 如图,在平面直角坐标系 中,点 在 轴上,点 在 轴上,且横坐标为 ,则点 的坐标为.
二、选择题
-
7. 下列各数中,是无理数的是( )A、 B、 C、 D、8. 在平面直角坐标系中,点 位于第四象限,距 轴2个单位长度,距 轴3个单位长度,则点 的坐标是( )A、 B、 C、 D、9. 给出下列4个命题:①经过直线外一点,有且只有一条直线与这条直线平行;②同旁内角互补;③如果直线 , a⊥b ,那么 ;④如果 ,那么 .其中假命题的个数有( )A、1个 B、2个 C、3个 D、4个10. 已知方程组 中, , 互为相反数,则 的值是( )A、0 B、-3 C、3 D、911. 下面解不等式 的过程中,有错误的一步是( )
①去分母得: ;②去括号得: ;③移项得: ,合并同类项得: ;④未知数的系数化为 得: .
A、① B、② C、③ D、④12. 大家知道 是无理数,而无理数是无限不循环小数,因此 的小数部分不可能全部写出来,但因为 ,即 ,所以可以用 来表示 的小数部分.如果 的小数部分是 , 的整数部分是 ,那么 的值是( )A、 B、 C、 D、13. 如图,将宽度相等的纸条沿 折叠一下,如果 ,那么 的度数是( ) A、70° B、100° C、110° D、140°14. 《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”这一章里,二元一次方程组是由算筹(算筹是中国古代用来记数、列式和进行演算的一种工具)来记录的.在算筹记数法中,以“立”“卧”两种排列方式来表示单位数目,表示两位数时,个位用立式,十位用卧式.如图(1),从左到右列出的算筹数分别表示 、 的系数与相应的常数项,根据图(1)可列出方程组 ,则根据图(2)列出的方程组是( )
A、70° B、100° C、110° D、140°14. 《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”这一章里,二元一次方程组是由算筹(算筹是中国古代用来记数、列式和进行演算的一种工具)来记录的.在算筹记数法中,以“立”“卧”两种排列方式来表示单位数目,表示两位数时,个位用立式,十位用卧式.如图(1),从左到右列出的算筹数分别表示 、 的系数与相应的常数项,根据图(1)可列出方程组 ,则根据图(2)列出的方程组是( )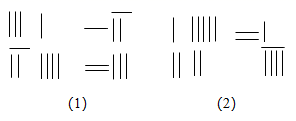 A、 B、 C、 D、
A、 B、 C、 D、三、解答题
-
15. 计算: .16. 解方程组:(1)、(2)、17. 解不等式或不等式组:(1)、解不等式 ,并求出它的最大整数解.(2)、解不等式组 ,并把它的解集在数轴上表示出来.18. 填写下列空格:
已知:如图, 平分 , .
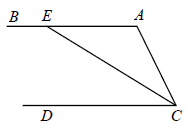
求证: .
证明: 平分 (已知),
_▲_ _▲_(_▲_).
(已知),
_▲_(_▲_).
(_▲_).
19. 某校有1800名学生.为了解全校学生的上学方式,该校数学兴趣小组经历了以下数据处理的一般过程:收集数据:在全校随机抽取120名学生进行抽样调查;
整理、描述数据:整理样本数据,得到频数分布表和统计图;
某校120名学生上学方式频数分布表
上学方式
频数
乘公共交通工具
40
步行
12
骑自行车
乘私家车
24
其它
8
合计
120
某校120名学生上学方式扇形统计图

分析数据:根据抽样调查结果,将估计出的全校1800名学生上学方式的情况绘制成条形统计图;
某校1800名学生上学方式条形统计图

得出结论:该校数学兴趣小组结合调查获取的信息,提出了一些建议.如:乘公共交通工具上学的人数较多,学校附近应建公共交通站台.
回答问题:
(1)、如果120名学生全部在七年级抽取,是否合理?(填“是”或“否”);频数分布表中 .(2)、计算出扇形统计图中“乘公共交通工具”部分的圆心角为多少度?(3)、补全条形统计图.(4)、请你结合上述统计的全过程,再提出一条合理化建议.20. 小明与他的爸爸一起做“投篮球”游戏,两人商定规则为:小明投中1个得3分,小明爸爸投中1个得1分.结果两人一共投中20个,经计算,发现两人得分恰好相等.你能知道他们两人各投中几个吗?21. 如图, 的三个顶点 、 、 都在小正方格的格点上,现将 向左平移5个单位,得到 . (1)、画出平移后的 (点 、 、 分别是 、 、 的对应点);(2)、写出 、 两点的坐标;(3)、计算 的面积;(4)、在图中连接 和 ,则这两条线段之间有什么关系?直接回答(不需要说理由).22. 点 是射线 上的一点,且不与 、 重合.
(1)、画出平移后的 (点 、 、 分别是 、 、 的对应点);(2)、写出 、 两点的坐标;(3)、计算 的面积;(4)、在图中连接 和 ,则这两条线段之间有什么关系?直接回答(不需要说理由).22. 点 是射线 上的一点,且不与 、 重合. (1)、如图,当点 在 之间时,过 点作 交直线 于点 ,过 点作 交直线 于点 .猜想 与 有什么数量关系,并说明理由.(2)、如备用图,当点 不在 之间时,画出 交直线 于点 , 交直线 于点 . 与 在(1)中的数量关系还成立吗?若不成立,写出你认为存在的数量关系(不需要说明理由).23. 某县为了推进“厕所革命”,改善农村生活卫生条件,雨甸村委会计划为400户居民修建 、 两种型号的三级污水处理厕所共25个,预计使用资金60万元(资金由政府出资一部分,其余由各户筹集).
(1)、如图,当点 在 之间时,过 点作 交直线 于点 ,过 点作 交直线 于点 .猜想 与 有什么数量关系,并说明理由.(2)、如备用图,当点 不在 之间时,画出 交直线 于点 , 交直线 于点 . 与 在(1)中的数量关系还成立吗?若不成立,写出你认为存在的数量关系(不需要说明理由).23. 某县为了推进“厕所革命”,改善农村生活卫生条件,雨甸村委会计划为400户居民修建 、 两种型号的三级污水处理厕所共25个,预计使用资金60万元(资金由政府出资一部分,其余由各户筹集).三级污水处理厕所的型号、修建费用、可供使用的户数如下表:
三级污水处理厕所
修建费用(万元/个)
可供使用户数
型
3
21
型
2
15
(1)、按计划可以修建 、 两种型号的三级污水处理厕所各几个?(2)、如果政府批给该村委会修建 型三级污水处理厕所不超过7个,求出满足要求的所有修建方案.(3)、在(2)的所有方案中,哪种方案最省钱?如果政府出资39万元,每户居民平均至少应筹集多少钱?