辽宁省朝阳市建平县2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-10-19 类型：期末考试

进入出卷网下载

一、选择题

1. 下列手机软件图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 新冠病毒需要放大多少倍我们才可以看到？病毒的整体尺寸一般在 $30 - 80 n m$ ，如果说仅仅可以看到， $10000$ 倍既可放大到肉眼可识别，这就需要运用专业的仪器设备-显微镜.生物学家发现一种病毒的长度约为 $0.000043$ 米，利用科学记数法表示为（）

A、 $4.3 \times 10^{6}$ 米 B、 $4.3 \times 10^{- 5}$ 米 C、 $4.3 \times 10^{- 6}$ 米 D、 $43 \times 10^{7}$ 米

查看试题解析
3. 事件：“在只装有2个红球和8个黑球的袋子里，摸出一个白球”是 $($ )

A、可能事件 B、随机事件 C、不可能事件 D、必然事件

查看试题解析
4. 如图， $a / / b$ ，点 $B$ 在直线 $b$ 上，且 $A B ⊥ B C ，$ 若 $∠ 1 = 34^{°} ，$ 则 $∠ 2$ 的大小为（）

A、34° B、54° C、56° D、66°

查看试题解析
5. 如图，在两个同心圆中，四条直径把大圆分成八等份，若往圆面投掷飞镖，则飞镖落在黑色区域的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{3}{10}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
6. 若 $a^{2} - 4 m a b + 4 b^{2}$ 是完全平方公式，则 $m$ 的值为（）

A、1 B、1或-1 C、2或－2 D、2

查看试题解析
7. 如图，△ABC中AB=AC，点D在AC边上，且BD=BC=AD，则∠A度数为（）

A、30° B、36° C、45° D、70°

查看试题解析
8. 作 $∠ A O B$ 平分线的作图过程如下：
作法：（1）在 $O A$ 和 $O B$ 上分别截取 $O D$ 、 $O E$ ，使 $O D = O E$ .（2）分别以 $D$ ， $E$ 为圆心，大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧交于点 $C$ .（3）作射线 $O C$ ，则 $O C$ 就是 $∠ A O B$ 的平分线.用下面的三角形全等的判定解释作图原理，最为恰当的是（）

A、 $S S S$ B、 $S A S$ C、 $A S A$ D、 $A A S$

查看试题解析
9. 请找出符合以下情景的图象：小颖将一个球被竖直向上抛起，球升到最高点后垂直下落，直到地面、在此过程中，球的速度与时间的关系的图象（）

A、 B、 C、 D、

查看试题解析
10. 如图，在等腰 $Δ$ ABC中，AB=AC，∠BAC=50°，∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合，则∠CEF的度数是（）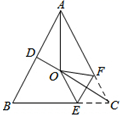

A、60° B、55° C、50° D、45°

查看试题解析

二、填空题

11. 已知一个角的补角是它余角的3倍，则这个角的度数为.

查看试题解析
12. 计算： $12 x^{3} y^{2} z \div (- 4 x^{2} y) =$ .

查看试题解析
13. 如果三条线段 $a, b, c$ 可组成三角形，且 $a = 3$ ， $b = 4$ ， $c$ 是奇数，则 $c =$ .

查看试题解析
14. 若 $a + b = 5, a b = - 3$ ，则 ${(a - b)}^{2}$ 的值为.

查看试题解析
15.
如图，AB∥CD，∠1=64°，FG平分∠EFC，则∠EGF=°．

查看试题解析
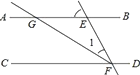16. 我国宋朝数学家杨辉在他的著作 $《$ 解：九章算法 $》$ 中提出“杨辉三角” $($ 如图 $)$ ，此图揭示了 ${(a + b)}^{n} (n$ 为非负整数 $)$ 展开式的项数及各项系数的有关规律.
例如： ${(a + b)}^{0} = 1$ ，它只有一项，系数为1；系数和为1；

${(a + b)}^{1} = a + b$ ，它有两项，系数分别为1，1，系数和为2；

${(a + b)}^{2} = a^{2} + 2 ab + b^{2}$ ，它有三项，系数分别为1，2，1，系数和为4；

${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 {ab}^{2} + b^{3}$ ，它有四项，系数分别为1，3，3，1，系数和为8； $\dots$ ，

则 ${(a + b)}^{n}$ 的展开式共有项，系数和为.

查看试题解析

三、解答题

17. ${(- \frac{1}{2})}^{- 2} - {(\frac{2}{3})}^{2019} \times {(- \frac{3}{2})}^{2020}$

查看试题解析
18. 如图，已知 $A D / / B C ， ∠ B = 25^{°} ， D B$ 平分 $∠ A D E ，$ 求 $∠ D E C$ 的度数.

查看试题解析
19. 现有三个村庄A，B，C，位置如图所示，线段AB，BC，AC分别是连通两个村庄之间的公路．现要修一个水站P，使水站不仅到村庄A，C的距离相等，并且到公路AB，AC的距离也相等，请在图中作出水站P的位置．（要求：尺规作图，不写作法，保留作图痕迹．）

查看试题解析
20. 学校举办“爱家乡山水”征文活动，小明为此次活动设计一个以三座山为背景的图标（如图），现用绿、红两种颜色对图标中的 $A ， B ， C$ 三块三角形区域分别涂色，一块区城只涂一种颜色.

(1)、请写出所有涂色的可能结果：

(2)、求这三块三角形区域中所涂颜色是“两块绿色、一块红色”的概率

查看试题解析
21. 如图，已如点 $C 、 E 、 B 、 F$ 在一条直线上， $A C / / F D ，$ $A C = F D ， C E = F B$ ，试问 $A B = D E$ 吗？如相等，请说明理由

查看试题解析
22. 为了解某种品牌小汽车的耗油量，我们对这种车在高速公路上做了耗油试验，并把试验的数据记录下来，制成如下表：

汽车行驶时间 $t / h$

0

1

2

3

···

邮箱剩余油量 $Q / L$

100

94

88

82

···

(1)、根据上表的数据，请你写出 $Q$ 与 $t$ 的关系式；

(2)、汽车行驶 $5 h$ 后，油箱中的剩余油量是多少？

(3)、该品牌汽车的油箱内加入 $48 L$ 汽油，若以 $100 k m / h$ 的速度匀速行驶，该车最多能行驶多远？

查看试题解析
23. 以点A为顶点作两个等腰直角三角形（△ABC，△ADE），如图1所示放置，使得一直角边重合，连接BD，CE．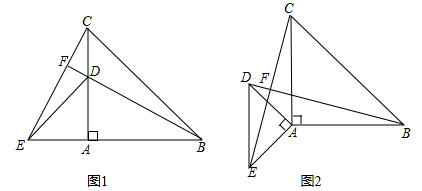

(1)、说明BD=CE；

(2)、延长BD，交CE于点F，求∠BFC的度数；

(3)、若如图2放置，上面的结论还成立吗？请简单说明理由．

查看试题解析
24. 如图表示甲骑摩托车和乙驾驶汽车沿相同的路线行驶 $9$ 千米，由 $A$ 地到 $B$ 地时，行驶的路程 $y$ （千米）与经过的时间 $x$ （小时）之间的关系.请根据图像填空

(1)、摩托车的速度为千米/小时：汽车的速度为小时；

(2)、汽车比摩托车早小时到达 $B$ 地.

(3)、在汽车出发后几小时，汽车和摩托车相遇？说明理由.

查看试题解析
25. 如图1，在 $△ A B C$ 中， $∠ B A C = 90^{°} ， A B = A C$ ，直线 $M N$ 过点 $A$ ，且 $M N / / B C$ ，点 $D$ 是直线 $M N$ 上一点，不与点 $A$ 重合.

(1)、若点 $E$ 是图1中线段 $A B$ 上一点，且 $D E = D A$ ，判断线段 $D E$ 与 $D A$ 的位置关系，并说明理由；

(2)、请在下面的 $A ， B$ 两题中任选题解答.
$A$ ：如图2，在（1）的条件下，连接， $B D$ 过点 $D$ 作 $D P ⊥ D B$ 交线段 $A C$ 于点 $P$ ，请判断线段 $D B$ 与 $D P$ 的数量关系，并说明理由；

$B$ ：如图3，在图1的基础上，改变点 $D$ 的位置后，连接 $B D$ ，过点 $D$ 作 $D P ⊥ D B$ 交线段 $C A$ 的延长线于点 $P$ ，请判断线段 $D B$ 与 $D P$ 的数量关系，并说明理由.

我选择：

查看试题解析

汽车行驶时间 $t / h$	0	1	2	3	···
邮箱剩余油量 $Q / L$	100	94	88	82	···