江苏省南京市建邺区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-10-19 类型：期末考试

进入出卷网下载

一、选择题

1. 下列命题中，是真命题的是（）

A、三角形的一条角平分线将三角形的面积平分 B、同位角相等 C、如果a²＝b² ，那么a＝b D、 $x^{2} - x + \frac{1}{4}$ 是完全平方式

查看试题解析
2. 甲型H1N1流感病毒的直径大约是0.000000081米，用科学记数法可表示为（）

A、8.1×10^﹣⁹米 B、8.1×10^﹣⁸米 C、81×10^﹣⁹米 D、0.81×10^﹣⁷米

查看试题解析
3. 已知方程组 ${\begin{matrix} 2 x + y = 7 \\ x + 2 y = 8 \end{matrix}$ ，那么x+y的值（）

A、-1 B、1 C、0 D、5

查看试题解析
4. 如图，若∠A+∠ABC=180°，则下列结论正确的是（）

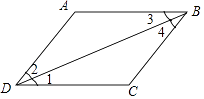A、∠1=∠2 B、∠2=∠3 C、∠1=∠3 D、∠2=∠4

查看试题解析
5. 根据需要将一块边长为 $x$ 的正方形铁皮按如图的方法截去一部分后，制成的长方形铁皮（阴影部分）的面积是多少？几名同学经过讨论给出了不同的答案，其中正确的是（）
① $(x - 5) (x - 6)$ ；② $x^{2} - 5 x - 6 (x - 5)$ ；③ $x^{2} - 6 x - 5 x$ ；④ $x^{2} - 6 x - 5 (x - 6)$

A、①②④ B、①②③④ C、① D、②④

查看试题解析
6. 某种药品说明书上，贴有如图所示的标签，则一次服用这种药品的计量范围是 $x ～ y m g$ ，则 $x ， y$ 的值分别为（）

用法用量：口服，每天 $30 ~ 60 m g$ .分 $2 ~ 3$ 次服用.

规格：□□□□□□

贮藏：□□□□□□

A、 $x = 15, y = 30$ B、 $x = 10, y = 20$ C、 $x = 15, y = 20$ D、 $x = 10, y = 30$

查看试题解析

二、填空题

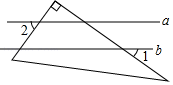
7. 计算：0.2⁵×5⁵＝.

查看试题解析
8. 已知一个多边形的内角和是720°，则这个多边形是边形.

查看试题解析
9. 若 $a > 0$ ，且 $a^{x} = 2$ ， $a^{y} = 3$ ，则 $a^{x - 2 y} =$ .

查看试题解析
10. 已知关于x，y的二元一次方程组 ${\begin{matrix} 2 x + 3 y = k \\ x + 2 y = - 1 \end{matrix}$ 的解互为相反数，则k的值是．

查看试题解析
11. 已知： ${\begin{array}{l} x = 2 + 3 t \\ y = 4 - t \end{array}$ ，则用x的代数式表示y为.

查看试题解析
12. 已知：（x+2）（x²﹣2ax+3）中不含x²项，a＝.

查看试题解析
13. 已知a∥b ，某学生将一直角三角板放置如图所示，如果∠1＝35°，则∠2的度数为．

查看试题解析
14. 已知 $x y = \frac{1}{2}$ ， $x - y = - 3$ ，则 $x^{2} y - x y^{2} =$ .

查看试题解析
15. 如图，已知 $B C$ 与 $D E$ 交于点 $M$ ，则 $∠ A + ∠ B + ∠ C + ∠ D + ∠ E + ∠ F$ 的度数为.

查看试题解析
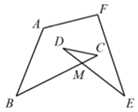16. 一副直角三角尺叠放如图1所示，现将45°的三角尺ADE固定不动，将含30°的三角尺ABC绕顶点A顺时针转动，使两块三角尺至少有一组边互相平行.如图2：当∠CAE＝15°时，BC∥DE.则∠CAE（0°＜∠CAE＜180°）其它所有可能符合条件的度数为.

查看试题解析

三、解答题

17. 计算：

(1)、 $2^{3} - {(π - 3)}^{0} + {(\frac{1}{2})}^{- 1} - {(- 2)}^{- 2}$ ；

(2)、先化简再求值： ${(2 a + 3)}^{2} + (a + 3) (a - 3) - 5 a^{2}$ 其中 $a = \frac{1}{2}$ .

查看试题解析
18. 因式分解

(1)、 $- 2 x^{2} + 4 x - 2$ ；

(2)、 $x^{2} (x - 2) + 4 (2 - x)$ .

查看试题解析
19. 解方程组： ${\begin{matrix} 2 x + y = 5, \\ x - 3 y = 6. \end{matrix}$

查看试题解析
20. 解不等式 $\frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 1$ ，把它的解集在数轴上表示出来，并求出这个不等式的负整数解.

查看试题解析
21. 如图，AB∥DG，∠1+∠2＝180°，

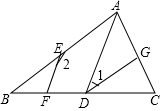(1)、求证：AD∥EF；

(2)、若DG是∠ADC的平分线，∠2＝150°，求∠B的度数．

查看试题解析
22. 在正方形网格中，每个小正方形的边长均为1个单位长度， $Δ A B C$ 的三个顶点的位置如图所示，现将 $Δ A B C$ 平移，使点 $A$ 变换为点 $A'$ ，点 $B' 、 C'$ 分别是 $B 、 C$ 的对应点.

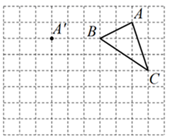(1)、请画出平移后的 $Δ A' B' C'$ ，并求 $Δ A' B' C'$ 的面积；

(2)、在图中找出所有的格点 $D$ ，使 $Δ A C D$ 的面积与 $Δ A B C$ 的面积相等.（若有多个点 $D$ ，则请用 $D_{1}$ 、 $D_{2}$ 、 $D_{3}$ 、…等标注）

查看试题解析
23.

(1)、若方程组 ${\begin{array}{l} 2 a - 3 b = 4.7 \\ 3 a + 5 b = 19.4 \end{array}$ 的解是 ${\begin{array}{l} a = 4.3 \\ b = 1.3 \end{array}$ ，则不解方程组写出方程组 ${\begin{array}{l} 2 (x - 1) - 3 (y + 1) = 4.7 \\ 3 (x - 1) + 5 (y + 1) = 19.4 \end{array}$ 的解为.

(2)、若关于 $x, y$ 的方程组 ${\begin{array}{l} 5 x + 3 a y = 16 \\ - b x + 4 y = 15 \end{array}$ ，（其中 $a, b$ 是常数）的解为 ${\begin{array}{l} x = 6 \\ y = 7 \end{array}$ ，解方程组 ${\begin{array}{l} 5 (x + 1) + 3 a (x - 2 y) = 16 \\ - b (x + 1) + 4 (x - 2 y) = 15 \end{array}$ .

(3)、若方程组 ${\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ 的解为 ${\begin{array}{l} x = 4 \\ y = 6 \end{array}$ ，则方程组 ${\begin{array}{l} 4 a_{1} x + 3 b_{1} y = 5 c_{1} \\ 4 a_{2} x + 3 b_{2} y = 5 c_{2} \end{array}$ 的解为.

查看试题解析
24. 某经销商经销的冰箱二月份的售价比一月份每台降价500元，已知卖出相同数量的冰箱一月份的销售额为9万元，二月份的销售额只有8万元.

(1)、二月份冰箱每台售价为多少元？

(2)、为了提高利润，该经销商计划三月份再购进洗衣机进行销售，已知洗衣机每台进价为4000元，冰箱每台进价为3500元，预计用不多于7.6万元的资金购进这两种家电共20台，设冰箱为y台（y≤12），请问有几种进货方案？

(3)、三月份为了促销，该经销商决定在二月份售价的基础上，每售出一台冰箱再返还顾客现金a元，而洗衣机按每台4400元销售，这种情况下，若（2）中各方案获得的利润相同，则a应取何值？

查看试题解析
25. 阅读佳佳与明明的对话，解决下列问题：

(1)、“多边形内角和为 $2020 °$ ”，为什么不可能？

(2)、佳佳求的是几边形的内角和？

(3)、错当成内角和那个外角为多少度？

查看试题解析
26. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ， $D$ 是 $A B$ 上一点，且 $∠ A C D = ∠ B$ .

(1)、求证： $C D ⊥ A B$ .
证明：在 $R t Δ A B C$ 中，

∵ $∠ A C B = 90 °$ （已知）

∴ $∠ A + ∠ B = 90 °$ （）

又∵ $∠ A C D = ∠ B$ （已知）

∴ $∠ A + ∠ A C D = 90 °$ （等量代换）

∴ $∠ A D C = 90 °$ （）

(2)、如图②，若 $∠ B A C$ 的平分线分别交 $B C$ ， $C D$ 于点 $E ， F$ ，求证： $∠ A E C = ∠ C F E$ .

(3)、如图③，若 $E$ 为 $B C$ 上一点， $A E$ 交 $C D$ 于点 $F$ ， $B C = 3 C E$ ， $A B = 4 A D$ ， $S_{Δ A B C} = 36$ .
①求 $S_{Δ C E F} - S_{Δ A D F}$ 的值；

②四边形 $B D F E$ 的面积是 ▲ .

查看试题解析