湖北省武汉市东湖高新区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-10-19 类型：期末考试

进入出卷网下载

一、选择题

1. 9的算术平方根是（）

A、 3 B、9 C、±3 D、±9

查看试题解析
2. 下列说法正确的是（）

A、无限小数都是无理数 B、有最小的正整数，没有最小的整数 C、a，b，c 是直线，若 a⊥b，b⊥c，则 a⊥c D、内错角相等

查看试题解析
3. 一元一次不等式组 ${\begin{array}{l} 2 x - 1 > x + 1 \\ x + 8 > 4 x - 1 \end{array}$ 的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，直线DE经过点A，DE∥BC，∠B＝44°，∠C＝57°，则∠BAC的度数是（）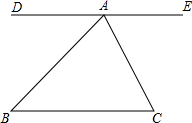

A、89° B、79° C、69° D、90°

查看试题解析
5. 下列调查中，适合用全面调查的是（）

A、调查某批次汽车的抗撞击能力 B、对端午节期间市场上粽子质量情况的调查 C、“神七”飞船发射前对重要零部件的检查 D、鞋厂检测生产的鞋底能承受的弯折次数

查看试题解析
6. 在平面直角坐标系中，点A(x，y)，B(3，4)，AB＝5，且AB∥x轴，则A点坐标为（）

A、(﹣3，4) B、(8，4) C、(3，9)或(﹣2，4) D、(﹣2，4)或(8，4)

查看试题解析
7. 若m＞n＞0，则下列结论正确的是（）

A、﹣2m＞﹣2n B、 $\frac{m}{x^{2} + 1}$ ＞ $\frac{n}{x^{2} + 1}$ C、 $\sqrt{m}$ ＜ $\sqrt{n}$ D、 $\frac{1}{3} m$ ＜ $\frac{1}{3} n$

查看试题解析
8. 将一箱苹果分给若干个小朋友，若每位小朋友分5个苹果，则还剩12个苹果；若每位小朋友分8个苹果，则有﹣个小朋友分到苹果但不到8个苹果．求这一箱苹果的个数与小朋友的人数．若设有x人，则可列不等式为（）

A、8（x﹣1）＜5x+12＜8 B、0＜5x+12＜8x C、0＜5x+12﹣8（x﹣1）＜8 D、8x＜5x+12＜8

查看试题解析
9. 如图，AB∥EF，∠ABP＝ $\frac{1}{4}$ ∠ABC，∠EFP＝ $\frac{1}{4}$ ∠EFC，已知∠FCD＝60°，则∠P的度数为（）

A、60° B、80° C、90° D、100°

查看试题解析
10. 若关于 $x$ 的不等式组 ${\begin{matrix} \frac{x - 1}{2} \geq 2 k \\ x - k \leq 4 k + 6 \end{matrix}$ 有解，且关于x的方程 $k x = 2 (x - 2) - (3 x + 2)$ 有非负整数解，则符合条件的所有整数k的和为（）

A、-5 B、-9 C、-12 D、-16

查看试题解析

二、填空题

11. $\sqrt{\frac{4}{9}}$ ＝；1﹣ $\sqrt[3]{3}$ 的相反数为；| $\sqrt{3}$ ﹣2|＝.

查看试题解析
12. 以方程组 ${\begin{array}{l} y = - x \\ 4 x + y = - 3 \end{array}$ 的解为坐标的点(x，y)在平面直角坐标系中的位置在第象限.

查看试题解析
13. 如图所示，数轴上表示2， $\sqrt{5}$ 的对应点分别为C、B，点C是AB的中点，则点A表示的数是。

查看试题解析
14. 打折前，买50件A商品和30件B商品用了920元，买60件A商品和10件B产品用了1000元.打折后，买400件A商品和400件B商品用了7500元，比不打折时少花的钱数为元.

查看试题解析
15. 如图，把一个长方形纸条 ABCD 沿 AF 折叠，已知∠ADB=28°，AE∥BD，则∠DAF=°.

查看试题解析
16. 如果点P(x，y)的坐标满足x＋y＝xy，那么称点P为“和谐点”，若某个“和谐点”到x轴的距离为3，则P点的坐标为.

查看试题解析
17. 解下列方程或方程组.

(1)、 ${\begin{array}{l} y = 3 x - 5 \\ 3 x - 5 y = 1 \end{array}$ ；

(2)、（x﹣1）²＝4.

查看试题解析
18. 如图，直线AB、CD相交于点O，且OE为∠BOC的平分线，DF∥OE，若∠AOC＝36°，求∠D的度数.

查看试题解析
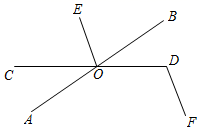19. 武汉市教育局为了解七年级学生在疫情期间参加体育锻炼的情况，随机抽样调查了某校七年级学生2020年4月某周参加体育锻炼的天数，并用得到的数据绘制了下面两幅不完整的统计图（如图），请你根据图中提供的信息，回答下列问题：

(1)、扇形统计图中a的值为， “锻炼时间为4天”的扇形所对圆心角的度数为，该校初一学生的总人数为；

(2)、补全条形统计图；

(3)、如果全市共有初一学生60000人，请你估计“锻炼时间不少于4天“的大约有多少人？

查看试题解析
20. 完成下面证明：已知：如图，AB和CD相交于点O，∠ACO＝∠COA，∠D＝∠BOD，过点C作CE∥AB且交DB的延长线于点 E.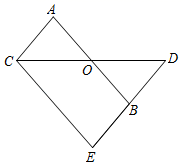

求证：∠A＝∠E.

证明：∵∠ACO＝∠COA，∠D＝∠BOD，

又∵∠COA＝∠BOD（   ），

∴∠ACO＝ ▲ ，

∴AC∥BD（   ），

∴∠A＝ ▲ （   ）.

又∵CE∥AB，

∴∠ABD＝ ▲ （   ），

∴∠A＝∠E（   ）.

查看试题解析
21. 如图，三角形COB是三角形AOB经过某种变化后得到的图形，观察点A与点C的坐标之间的关系.三角形AOB内任意一点M的坐标为(x，y)，点M经过这种变化后得到点N.

(1)、点N的坐标为；

(2)、将△ABC先向左平移2个单位长度，再向上平移1个单位长度，得到△A′B′C′，在图中画出三角形△A′B′C′，△A′B′C′的面积为；

(3)、直线BC交y轴于点D，则点D的坐标为.

查看试题解析
22.

(1)、一个长方形纸片的长减少3cm，宽增加2cm，就成为一个正方形纸片，并且长方形纸片周长的3倍比正方形纸片周长的2倍多30cm.这个长方形纸片的长、宽各是多少？

(2)、小明同学想用（1）中得到的正方形纸片，沿着边的方向裁出一块面积为30cm²的长方形纸片，使它的长宽之比为3∶2.请问小明能用这块纸片裁出符合要求的纸片吗？请说明理由.

查看试题解析
23. 如图，四边形ABCD中，AB∥CD，∠B＝∠D，点E为BC延长线上一点，连接AE，AE交CD于H.∠DCE的平分线交AE于G.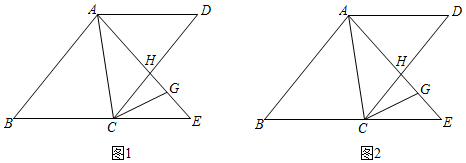

(1)、求证：AD∥BC；

(2)、若∠BAC＝∠DAE，∠AGC＝2∠CAE.求∠CAE的度数；

(3)、（2）中条件∠BAC＝∠DAE仍然成立，若∠AGC＝3∠CAE，直接写出∠CAE的度数.

查看试题解析
24. 在平面直角坐标系中，已知A(a，0)，B(b，0)，C(0，4)，D(6，0).点P(m，n)为线段CD上一点（不与点C和点D重合）.

(1)、利用三角形COP、三角形DOP及三角形COD之间的面积关系，求m与n之间的数量关系；

(2)、如图1，若a＝﹣2，点B为线段AD的中点，且三角形ABC的面积等于四边形AOPC面积，求m的值；

(3)、如图2，设a，b，m满足 ${\begin{array}{l} 2 a + 3 b + m = 0 \\ 3 a + 2 b + m = - 5 \end{array}$ ，若三角形ABP的面积小于5，求m的取值范围.

查看试题解析