甘肃省陇南市徽县2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-10-19 类型：期末考试

进入出卷网下载

一、选择题

1. 在平面直角坐标系中，点P（3，﹣2）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 在数轴上表示不等式 $x + 4 \geq 2$ 的解集，正确的是（）

A、 B、 C、 D、

查看试题解析
3. 下列说法中正确的是（）

A、 $\sqrt{36}$ 的平方根是±6 B、 $\sqrt{16}$ 的平方根是±2 C、|﹣8|的立方根是﹣2 D、 $\sqrt{16}$ 的算术平方根是4

查看试题解析
4. 如图，已知∠1＝∠B，∠2＝∠C，则下列结论不成立的是（）

A、∠B＝∠C B、AD∥BC C、∠2＋∠B＝180° D、AB∥CD

查看试题解析
5. 若 $m = \sqrt{40} - 5$ ，则估计 $m$ 的值所在的范围是（）

A、 $1 < m < 2$ B、 $2 < m < 3$ C、 $3 < m < 4$ D、 $4 < m < 5$

查看试题解析
6. 南阳市中心城区参加中招考试考生有25000名，为了解“一调”数学考试情况从中随机抽取了1800名学生的成绩进行统计分析，下面叙述正确的是（）

A、25000名学生是总体，每名学生是总体的一个个体 B、1800名学生的成绩是总体的一个样本 C、样本容量是25000 D、以上调查是全面调查

查看试题解析
7. 如图， $A B // C D ， ∠ B A E = 120 ° ， ∠ D C E = 30 °$ ，则 $∠ A E C =$ _______度.（）

A、70 B、150 C、90 D、100

查看试题解析
8. 关于x的不等式组 ${\begin{array}{l} 2 x < 3 (x - 3) + 1 \\ \frac{3 x + 2}{4} > x + a \end{array}$ 有四个整数解，则a的取值范围是（）

A、﹣ $\frac{11}{4}$ ＜a≤﹣ $\frac{5}{2}$ B、﹣ $\frac{11}{4}$ ≤a＜﹣ $\frac{5}{2}$ C、﹣ $\frac{11}{4}$ ≤a≤﹣ $\frac{5}{2}$ D、﹣ $\frac{11}{4}$ ＜a＜﹣ $\frac{5}{2}$

查看试题解析
9. 《九章算术》有题曰：“今有五雀，六燕，集称之衡，雀俱重，燕俱轻.一雀一燕交而处，衡适平，并燕雀重一斤，问燕雀一枚各重几何？ ”其大意是：“现在有5只雀， 6只燕，分别集中放在天平上称重，聚在一起的雀重燕轻.将一只雀一只燕交换位置而放，重量相等，5只雀、6只燕重量共一斤，问雀和燕各重多少？”古代记1斤为16两，则设1只雀 $x$ 两，一只燕 $y$ 两，可列出方程组为（）

A、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 4 x + y = 5 y + x \end{array}$ B、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 5 x = 6 y \end{array}$ C、 ${\begin{array}{l} 5 x + 6 y = 10 \\ 4 x + y = 5 y + x \end{array}$ D、 ${\begin{cases} 5 x + 6 y = 10 \\ 5 x = 6 y \end{cases}$

查看试题解析

二、填空题

10. 若 $\sqrt{x} + \sqrt{- x}$ 有意义,则 $\sqrt{x + 1} =$ ．

查看试题解析
11. 在 $y = k x + b$ 中，当 $x = 1$ 时， $y = 2$ ；当 $x = 2$ 时， $y = 4$ ，则 $k =$ ， $b =$ .

查看试题解析
12. 在平面直角坐标系内，把 $P (- 5, - 2)$ ，先向左平移2个单位长度，再向上平移4个单位长度后得到的点的坐标是.

查看试题解析
13. 若（m﹣3）x＜3﹣m的解集为x＞﹣1，则m的取值范围为.

查看试题解析
14. 如图，直线AB，CD相交于点O，OE⊥AB，O为垂足，∠EOD=26°，则∠AOC= ， ∠COB=.

查看试题解析
15. 若 $\sqrt{a + b + 5} + | 2 a - b + 1 | = 0$ ，则（b﹣a）²⁰¹⁵＝．

查看试题解析
16. 把方程组 ${\begin{array}{l} x + 2 y = 1 + m \\ 2 x + y = 3 \end{array}$ 中，若未知数 $x 、 y$ 满足 $x + y > 0$ ，则 $m$ 的取值范围是.

查看试题解析
17. 如图，把一张长方形纸条按图中那样折叠后，若得到∠AOB′=70°，则∠OGC=.

查看试题解析
18. 已知 $y = 3 x y + x$ ，求代数式 $\frac{2 x + 3 x y - 2 y}{x - 2 x y - y} =$ .

查看试题解析
19. 如图，直角坐标平面 $x O y$ 内，动点 $P$ 按图中箭头所示方向依次运动，第1次从点 $(- 1 ， 0)$ 运动到点 $(0 ， 1)$ ，第2次运动到点 $(1 ， 0)$ ，第3次运动到点 $(2 ， - 2)$ ，……，按这样的运动规律，动点 $P$ 第2018次运动到点的坐标是.

查看试题解析

三、解答题

20. 计算： $\sqrt{9} + \sqrt[3]{- 125} + | \sqrt{3} - 2 |$ .

查看试题解析
21. 解方程组：
① ${\begin{array}{l} 2 x - y = 5 \\ x + 2 y = 5 \end{array}$

② ${\begin{array}{l} \frac{x + 3 y}{2} = \frac{3}{5} \\ 5 (x - 2 y) = - 4 \end{array}$

查看试题解析
22. 求出下列不等式组的解集，并在数轴上表示出来：
${\begin{array}{l} 7 (x - 5) + 2 (x + 1) > - 15 \\ \frac{2 x + 1}{3} - \frac{3 x - 1}{2} < 0 \end{array}$

查看试题解析
23. 已知△ABC的三个顶点的坐标分别是 $A (0 ， 1)$ ， $B (2 ， 0)$ ， $C (2 ， 3)$ .

(1)、在所给的平面直角坐标系 $x O y$ 中画出 $Δ A B C$ ， $Δ A B C$ 的面积为；

(2)、点 $P$ 在 $x$ 轴上，且 $Δ A B P$ 的面积等于 $Δ A B C$ 的面积，求点 $P$ 的坐标.

查看试题解析
24. 某学校在暑假期间开展“心怀感恩，孝敬父母”的实践活动，倡导学生在假期中帮助父母干家务.开学以后，校学生会随机抽取了部分学生，就暑假“平均每天帮助父母干家务所用时长”进行了调查，以下是根据相关数据绘制的统计图的一部分：

根据上述信息，回答下列问题：

(1)、在本次随机抽取的样本中，调查的学生人数是人；

(2)、 $m =$ ， $n =$ ；

(3)、补全频数分布直方图；

(4)、如果该校共有学生2000人，请你估计“平均每天帮助父母干家务的时长不少于30分钟”的学生大约有多少人？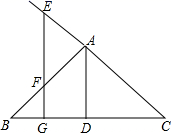

查看试题解析
25. 如图，已知 $A D$ 平分 $∠ B A C$ ，且 $A D ⊥ B C$ 于 $D$ ，点 $E 、 A 、 C$ 在同一直线上， $∠ D A C = ∠ E F A$ ，延长 $E F$ 交 $B C$ 于 $G$ ，证明： $E G ⊥ B C$ .

查看试题解析
26. 某文具店购进A、B两种文具进行销售.若每个A种文具的进价比每个B种文具的进价少2元，且用900元正好可以购进50个A种文具和50个B种文具，

(1)、求每个A种文具和B种文具的进价分别为多少元？

(2)、若该文具店购进A种文具的数量比购进 $B$ 种文具的数量的3倍还少5个，购进两种文具的总数量不超过95个，每个A种文具的销售价格为12元，每个B种文具的销售价格为15元，则将购进的A、B两种文具全部售出后，可使总利润超过371元，通过计算求出该文具店购进A、B两种文具有哪几种方案？

查看试题解析