云南省曲靖市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-10-19 类型:期末考试
一、填空题
-
1. 若二次根式 有意义,则x的取值范围是 .2. 一次函数 的图象不经过第象限.3. 如图,在四边形ABCD中,点P是对角线BD的中点,点 分别是AB,CD的中点, , ,则 的度数是.
 4. 如图,在 中, , , ,交 于点 ,且 ,则 .
4. 如图,在 中, , , ,交 于点 ,且 ,则 . 5. 如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是.
5. 如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是.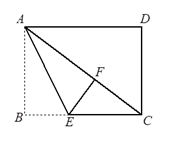 6. 如图, 于点A, 于点B,点P为线段AB上任意一点,若 , , ,则 的最小值是.
6. 如图, 于点A, 于点B,点P为线段AB上任意一点,若 , , ,则 的最小值是.
二、选择题
-
7. 下列数字中,属于最简二次根式的是( )A、 B、 C、 D、8. 下列计算错误的是( )A、 ﹣ = B、 ÷2= C、 D、3+2 =59. 由线段 组成的三角形不是直角三角形的是( )A、 B、 C、 D、10. 下列命题中正确的是( )A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是菱形 D、两条对角线互相垂直且平分的四边形是正方形11. 把函数y=x向上平移3个单位,下列在该平移后的直线上的点是( )A、 B、 C、 D、12. 在某校举行的“我的中国梦”演讲比赛中,10名参赛学生的成绩统计如图所示,对于这10名学生的参赛成绩,下列说法中正确的是( )
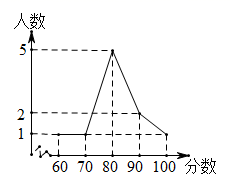 A、平均数是80分 B、众数是5 C、中位数是80分 D、方差是11013. 已知点 , 都在直线 上,则 大小关系是( )A、 B、 C、 D、不能比较14. 如图,在 中, , , ,点 为 的中点,延长 至 点,使 ,则 的面积是( )
A、平均数是80分 B、众数是5 C、中位数是80分 D、方差是11013. 已知点 , 都在直线 上,则 大小关系是( )A、 B、 C、 D、不能比较14. 如图,在 中, , , ,点 为 的中点,延长 至 点,使 ,则 的面积是( ) A、 B、 C、8 D、
A、 B、 C、8 D、三、解答题
-
15. 计算:(1)、(2)、16. 先化简,再求值: ,其中 .17. 如图,在平面直角坐标系内,直线AB与 轴交于点 ,与 轴交于点 .
 (1)、求直线AB的解析式;(2)、若直线AB上的点C在第一象限,且 ,求点C的坐标.18. 初中生的体育锻炼问题一直是社会关注的焦点之一,为此某教育局对该县某校八年级学生的体育锻炼时间进行一次抽样调查(分为三个等级,A级:每天能坚持体育锻炼两个小时;B级:每天能坚持体育锻炼一个小时;C级:每天很少进行体育锻炼),并将调查结果绘制成图①和图②的统计图(不完整).
(1)、求直线AB的解析式;(2)、若直线AB上的点C在第一象限,且 ,求点C的坐标.18. 初中生的体育锻炼问题一直是社会关注的焦点之一,为此某教育局对该县某校八年级学生的体育锻炼时间进行一次抽样调查(分为三个等级,A级:每天能坚持体育锻炼两个小时;B级:每天能坚持体育锻炼一个小时;C级:每天很少进行体育锻炼),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
 (1)、此次抽样调查中,共调查了多少名学生?(2)、求出扇形统计图②中A级所对应的圆心角的度数,并补全条形统计图①;(3)、根据抽样调查结果,请你估计该县8000名初中生大约有多少名学生体育锻炼的时间达标(达标包括A级和B级)?19. 如图,在正方形ABCD中,正方形的边长为 , 是 的中点,F是CD上一点,且 ,判断 的形状并说明理由.
(1)、此次抽样调查中,共调查了多少名学生?(2)、求出扇形统计图②中A级所对应的圆心角的度数,并补全条形统计图①;(3)、根据抽样调查结果,请你估计该县8000名初中生大约有多少名学生体育锻炼的时间达标(达标包括A级和B级)?19. 如图,在正方形ABCD中,正方形的边长为 , 是 的中点,F是CD上一点,且 ,判断 的形状并说明理由. 20. 观察以下等式:
20. 观察以下等式:第1个等式:
第2个等式:
第3个等式:
第4个等式:
第5个等式:
按照以上规律,解决下列问题:
(1)、写出第7个等式:;(2)、写出你猜想的第 个等式:(用含 的等式表示),并证明.21. 如图①,四边形ABCD中,对角线AC,BD相交于点 , , ,且 . (1)、求证:四边形ABCD是矩形;(2)、以 三点为顶点,求作菱形 .
(1)、求证:四边形ABCD是矩形;(2)、以 三点为顶点,求作菱形 .小明的作法:如图②,过D点 ,过C点作 ,两线交于点P,则四边形 为所求作的菱形.
①请证明小明所作的四边形 是菱形;
②若 , ,求四边形 的面积.
22. 受疫情影响,全国中小学延迟开学,很多学校都开展起了“线上教学”,市场上对电脑的需求激增.某厂家准备3月份紧急生产A、B两种型号的电脑,其中A型号电脑每台的利润为600元,B型号电脑每台的利润为800元.该厂家计划生产两种型号的电脑共100台,其中生产A型号电脑的数量不少于B型号电脑数量的2倍,设生产了A型号电脑x台,这100台电脑的销售总利润为y元.(1)、求y关于x的函数关系式;(2)、该厂家生产A型号、B型号电脑各多少台,才能使销售总利润最大?最大利润是多少?23. 如图,在平面直角坐标系中,直线 与 轴、 轴分别交于 两点. (1)、求出 两点的坐标;(2)、 为 轴上一点,将直线AC沿着直线AB平移,使得点A落在点B处,此时点C的对应点为D,求出点D的坐标,请判断四边形ABDC的形状,并说明理由.(3)、点M为 轴上一点,点N为坐标平面内另一点,若以 为顶点的四边形是菱形,请求出所有符合条件的点N的坐标.
(1)、求出 两点的坐标;(2)、 为 轴上一点,将直线AC沿着直线AB平移,使得点A落在点B处,此时点C的对应点为D,求出点D的坐标,请判断四边形ABDC的形状,并说明理由.(3)、点M为 轴上一点,点N为坐标平面内另一点,若以 为顶点的四边形是菱形,请求出所有符合条件的点N的坐标.