云南省昆明市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-10-19 类型:期末考试
一、填空题
-
1. 函数 有意义的 的取值范围是.2. 如图,在四边形 中, ,要使四边形 成为平行四边形,则应增加的条件是(写一个即可).
 3. 一组数据:-2,1,1,0,2,则这组数据的众数是.4. 直线 与 轴交点坐标为.5. 如图,矩形 的对角线 与 相交点 , , 、 分别为 、 的中点,则 的长度为.
3. 一组数据:-2,1,1,0,2,则这组数据的众数是.4. 直线 与 轴交点坐标为.5. 如图,矩形 的对角线 与 相交点 , , 、 分别为 、 的中点,则 的长度为. 6. 已知 是 的边 上的高,若 , , ,则 的长为.
6. 已知 是 的边 上的高,若 , , ,则 的长为.二、选择题
-
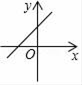
7. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、8. 下列命题正确的是( )A、平行四边形的对角线互相垂直平分 B、矩形的对角线互相垂直平分 C、菱形的对角线互相平分且相等 D、正方形的对角线互相垂直平分9. 若b>0,则一次函数y=﹣x+b的图象大致是( )A、
 B、
B、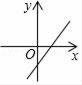 C、
C、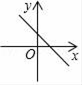 D、
D、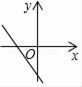 10. 考察五位学生的学习情况,得到五个各不相同的数据,统计时,出现了一处错误:将最好成绩写得更高了.计算结果不受影响的是( )A、中位数 B、加权平均数 C、方差 D、平均数11. 如图,矩形 的边 长为 ,边 长为 , 在数轴上,以原点 为圆心,对角线 的长为半径画弧,交正半轴于一点,则这个点表示的实数是( )
10. 考察五位学生的学习情况,得到五个各不相同的数据,统计时,出现了一处错误:将最好成绩写得更高了.计算结果不受影响的是( )A、中位数 B、加权平均数 C、方差 D、平均数11. 如图,矩形 的边 长为 ,边 长为 , 在数轴上,以原点 为圆心,对角线 的长为半径画弧,交正半轴于一点,则这个点表示的实数是( ) A、 B、 C、 D、12. 已知点 , , , 分别是菱形 各边的中点,则四边形 一定是( )A、正方形 B、矩形 C、菱形 D、非平行四边形13. 如图,一个函数的图象由射线 、线段 、射线 组成,其中点 , , , ,则下列表述正确的是( )
A、 B、 C、 D、12. 已知点 , , , 分别是菱形 各边的中点,则四边形 一定是( )A、正方形 B、矩形 C、菱形 D、非平行四边形13. 如图,一个函数的图象由射线 、线段 、射线 组成,其中点 , , , ,则下列表述正确的是( ) A、当 时, 随 的增大而增大 B、当 时, 随 的增大而减小 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小14. 在周长为 的正方形 中,点 是 边的中点,点 为对角线 上的一个动点,则 的最小值为( )
A、当 时, 随 的增大而增大 B、当 时, 随 的增大而减小 C、当 时, 随 的增大而增大 D、当 时, 随 的增大而减小14. 在周长为 的正方形 中,点 是 边的中点,点 为对角线 上的一个动点,则 的最小值为( )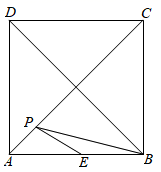 A、2 B、 C、 D、
A、2 B、 C、 D、三、解答题
-
15. 计算下列各题(1)、(2)、16. 先化简,再求值: ,其中 ,17. 如图,在□ ABCD中,点E、F在对角线BD上,且BE=DF.
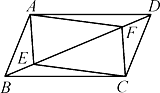 (1)、求证:AE=CF;(2)、求证:四边形AECF是平行四边形.18. 如图,直角坐标系 中,一次函数 的图象 分别与 、 轴交于 , 两点,正比例函数的图象 与 交于点 ,求 的值及 的表达式.
(1)、求证:AE=CF;(2)、求证:四边形AECF是平行四边形.18. 如图,直角坐标系 中,一次函数 的图象 分别与 、 轴交于 , 两点,正比例函数的图象 与 交于点 ,求 的值及 的表达式. 19. 学校开展一次知识竞赛活动,满分 分,学生得分均为整数, 分及以上为合格, 分及以上为优秀,每组参赛人员都是 人.甲、乙两组学生竞赛成绩统计分析表和成绩分布折线统计图如下列图表所示:
19. 学校开展一次知识竞赛活动,满分 分,学生得分均为整数, 分及以上为合格, 分及以上为优秀,每组参赛人员都是 人.甲、乙两组学生竞赛成绩统计分析表和成绩分布折线统计图如下列图表所示:成绩统计分析表
组别
平均分
中位数
合格率
优秀率
甲组
7.5
80%
20%
乙组
6.6
90%
10%
成绩分布折线统计图
 (1)、求出成绩统计分析表中 、 的值;(2)、甲、乙两组成绩的方差哪个大?请简要说明判断理由.20. 如图,在四边形 中,点 是对角线 的中点, , , , . 是直角三角形吗?若是请说明理由.
(1)、求出成绩统计分析表中 、 的值;(2)、甲、乙两组成绩的方差哪个大?请简要说明判断理由.20. 如图,在四边形 中,点 是对角线 的中点, , , , . 是直角三角形吗?若是请说明理由. 21. 某儿童娱乐项目推出两种付费方式.方式一:先购买会员证,每张会员证 元,只限本人凭证娱乐,每次再付费 元;方式二:不购买会员证,每次付费 元.
21. 某儿童娱乐项目推出两种付费方式.方式一:先购买会员证,每张会员证 元,只限本人凭证娱乐,每次再付费 元;方式二:不购买会员证,每次付费 元.设小华计划今年娱乐次数为 ( 为正整数)
(1)、根据题意,填写下表:今年娱乐次数
5
10
20
方式一的总费用(元)
120
140
方式二的总费用(元)
40
80
(2)、若小华计划今年娱乐的总费用为192元,选择哪种付费方式,他娱乐的次数比较多?(3)、当 时,小华选择哪种付费方式更合算?并说明理由22. 在一次科学实验中,测得某物体的初始温度为 .现以每秒 的速度下降.设经过的时间为 秒,物体的温度为 .物体的温度随时间变化规律的函数解析式为 ,函数大致图象如图1所示. (1)、几秒后物体的温度变为 ?
(1)、几秒后物体的温度变为 ?对于这个问题
①从方程的角度看,实际上就是求方程:的解;
②从图象的角度看,就是求函数图象与 轴交点的坐标;
③从函数解析式的角度看,就是求函数值为时,对应的 值.
④基于以上分析与思考,可得到:秒后物体的温度变为 .
(2)、请运用以上方法解决如下问题:
函数 的图象如图2所示,则方程 的解为.
23. 如图,在平面直角坐标系中,四边形 是矩形,点 的坐标为 ,点 的坐标为 ,把矩形 沿 折叠,点 落在点 处, 交 于点 . (1)、求证: ;(2)、求 的面积;(3)、求点 的坐标.
(1)、求证: ;(2)、求 的面积;(3)、求点 的坐标.