青海省西宁市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-10-19 类型:期末考试
一、选择题
-
1. 计算 的结果是( )A、﹣3 B、3 C、﹣9 D、92. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、3. 如图是西宁市某周内最高气温的折线统计图,关于这 天的日最高气温的说法正确的是( )
 A、极差是 B、众数是 C、中位数是 D、平均数是4. 小明骑自行车上学,开始以正常速度匀速行驶,但行至途中自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了骑车速度.下面是小明距离学校的路程 关于行驶时间 的函数图象,那么符合小明行驶情况的图象大致是( )A、
A、极差是 B、众数是 C、中位数是 D、平均数是4. 小明骑自行车上学,开始以正常速度匀速行驶,但行至途中自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了骑车速度.下面是小明距离学校的路程 关于行驶时间 的函数图象,那么符合小明行驶情况的图象大致是( )A、 B、
B、 C、
C、 D、
D、 5. 已知点 都在直线 上,则 的大小关系是( )A、 B、 C、 D、6. 如图,在长方形 中无重叠放入面积分别为 和 的两张正方形纸片,则图中空白部分的面积为( )
5. 已知点 都在直线 上,则 的大小关系是( )A、 B、 C、 D、6. 如图,在长方形 中无重叠放入面积分别为 和 的两张正方形纸片,则图中空白部分的面积为( ) A、 B、 C、 D、7. 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
A、 B、 C、 D、7. 明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )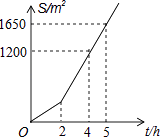 A、300m2 B、150m2 C、330m2 D、450m2
A、300m2 B、150m2 C、330m2 D、450m2二、填空题
-
8. 若代数式 在实数范围内有意义,则x的取值范围是。9. 若函数 是正比例函数,则 .10. 化简: .11. 如图,已知函数y1=kx-1和y2=x-b的图象交于点P(-2,-5),则根据图象可得不等式kx-1>x-b的解集是 .
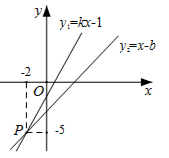 12. 如图,在 中,已知 ,点 分别是 的中点.则四边形 的周长是.
12. 如图,在 中,已知 ,点 分别是 的中点.则四边形 的周长是. 13. 已知两条线段的长为5cm和12cm,当第三条线段的长为cm时,这三条线段能组成一个直角三角形.14. 如图,在平面直角坐标系中,四边形 是菱形,若点 的坐标是 ,则点 的坐标是.
13. 已知两条线段的长为5cm和12cm,当第三条线段的长为cm时,这三条线段能组成一个直角三角形.14. 如图,在平面直角坐标系中,四边形 是菱形,若点 的坐标是 ,则点 的坐标是. 15. 如图, 中, ,将 折叠,使 点与 的中点 重合,折痕为 则线段 的长为.
15. 如图, 中, ,将 折叠,使 点与 的中点 重合,折痕为 则线段 的长为.
三、解答题
-
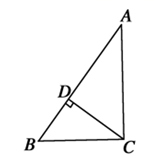
16. 计算:17. 计算:18. 如图,在 中, 于点 .求 的长.
 19. 如图,在 中, 是它的一条对角线,过 两点分别作 ,垂足分别为 ,延长 分别交 于点 .求证:四边形 是平行四边形.
19. 如图,在 中, 是它的一条对角线,过 两点分别作 ,垂足分别为 ,延长 分别交 于点 .求证:四边形 是平行四边形.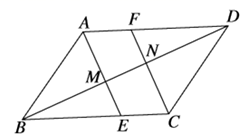 20. 下面是某公司 名员工每人所创的年利润(单位:万元):(1)、完成下列表格.
20. 下面是某公司 名员工每人所创的年利润(单位:万元):(1)、完成下列表格.每人所创年利润(万元)
3
5
8
10
人数
3
4
(2)、这组数据的中位数是 , 众数是;(3)、这个公司平均每人所创年利润是多少万元?21. 如图,在四边形 中, , ,对角线 , 交于点 , 平分 ,过点 作 交 的延长线于点 ,连接 . (1)、求证:四边形 是菱形;(2)、若 , ,求 的长.
(1)、求证:四边形 是菱形;(2)、若 , ,求 的长.
22. 某学校积极响应怀化市“三城同创”的号召,绿化校园,计划购进A,B两种树苗,共21棵,已知A种树苗每棵90元,B种树苗每棵70元.设购买A种树苗x棵,购买两种树苗所需费用为y元.(1)、求y与x的函数表达式,其中0≤x≤21;(2)、若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.23. 如图,在平面直角坐标系中,一次函数 与 轴, 轴分别交于点 和 一次函数 与 轴, 轴分别交于点 和 这两个函数图象交于点 . (1)、求 点坐标;(2)、求 的面积;(3)、设点 在 轴上,且与 构成等腰三角形,请直接写出所有符合条件的点 的坐标.
(1)、求 点坐标;(2)、求 的面积;(3)、设点 在 轴上,且与 构成等腰三角形,请直接写出所有符合条件的点 的坐标.