辽宁省朝阳市建平县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-10-19 类型:期末考试
一、选择题
-
1. 不等式 的解集是( )A、 B、 C、 D、2. 若分式 中的 、 的值都变为原来的3倍,则此分式的值( )A、不变 B、是原来的3倍 C、是原来的 D、是原来的3. 下列图案中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 多项式 各项的公因式是( )A、 B、 C、 D、5. 如图,在四边形ABCD中,AB=CD,M,N,P分别是AD,BC,BD的中点,若∠MPN=130°,则∠NMP的度数为( )
4. 多项式 各项的公因式是( )A、 B、 C、 D、5. 如图,在四边形ABCD中,AB=CD,M,N,P分别是AD,BC,BD的中点,若∠MPN=130°,则∠NMP的度数为( )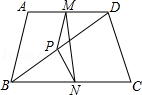 A、10° B、15° C、25° D、40°6. 如果一个多边形的每一个内角都是 ,那么这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形7. 如图, 中, 的垂直平分线 交 于 ,如果 , ,那么 的周长是( )
A、10° B、15° C、25° D、40°6. 如果一个多边形的每一个内角都是 ,那么这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形7. 如图, 中, 的垂直平分线 交 于 ,如果 , ,那么 的周长是( ) A、 B、 C、 D、8. 若解分式方程 = 产生增根,则m=( )A、1 B、0 C、﹣4 D、﹣59. 下列命题中是真命题的是( )A、若 ,则 B、有两个角为 的三角形是等边三角形 C、一组对边相等,另一组对边平行的四边形是平行四边形 D、如果 ,那么 ,10. 如图,在 中, , ,将 绕点 逆时针旋转 ,得到 ,连接 ,则 的长是( )
A、 B、 C、 D、8. 若解分式方程 = 产生增根,则m=( )A、1 B、0 C、﹣4 D、﹣59. 下列命题中是真命题的是( )A、若 ,则 B、有两个角为 的三角形是等边三角形 C、一组对边相等,另一组对边平行的四边形是平行四边形 D、如果 ,那么 ,10. 如图,在 中, , ,将 绕点 逆时针旋转 ,得到 ,连接 ,则 的长是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式: .12. 关于x的不等式组 的解集为-3<x<3, 则a,b的值分别为.13.
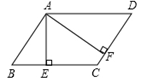
如图,在□ 中, ⊥ 于点 , ⊥ 于点 .若 , ,且□ 的周长为40,则□ 的面积为。
 14. 张明与李强共同清点一批图书,已知张明清点完200本图书所用的时间与李强清点完300本图书所用的时间相同,且李强平均每分钟比张明多清点10本,则张明平均每分钟清点图书的数量本.15. 如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=度.
14. 张明与李强共同清点一批图书,已知张明清点完200本图书所用的时间与李强清点完300本图书所用的时间相同,且李强平均每分钟比张明多清点10本,则张明平均每分钟清点图书的数量本.15. 如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA=度. 16. 如图,矩形ABCD的面积为20cm2 , 对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为 .
16. 如图,矩形ABCD的面积为20cm2 , 对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为 .
三、解答题
-
17. 先化简,再求值: .其中 , .18. 解不等式组: ,并把它的解集在数轴上表示出来
 19. 解分式方程: .20. 如图是一种儿童的游乐设施—儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.
19. 解分式方程: .20. 如图是一种儿童的游乐设施—儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由. 21. 某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.(1)、求甲、乙两种商品每件的价格各是多少元?(2)、计划购买这两种商品共50件,且投入的经费不超过3200元,那么最多购买多少件甲种商品?22. 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的格点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1 , 然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
21. 某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.(1)、求甲、乙两种商品每件的价格各是多少元?(2)、计划购买这两种商品共50件,且投入的经费不超过3200元,那么最多购买多少件甲种商品?22. 如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的格点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1 , 然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2. (1)、在网格中画出△A1B1C1和△A1B2C2;(2)、计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)23. 如图,在 中, 平分 , , 交 的延长线于点 ,点 在 上,且 ,求证:点 是 的中点.
(1)、在网格中画出△A1B1C1和△A1B2C2;(2)、计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)23. 如图,在 中, 平分 , , 交 的延长线于点 ,点 在 上,且 ,求证:点 是 的中点. 24. 如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
24. 如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s). (1)、用含t的代数式表示:AP= cm;DP= cm;BQ= cm;CQ= cm.(2)、当t为何值时,四边形APQB是平行四边形?(3)、当t为何值时,四边形PDCQ是平行四边形?25. 为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造 两种型号的沼气池共20个,以解决该村所有农户的燃料问题,两种型号沼气池的占地面积、使用农户数及造价见下表:
(1)、用含t的代数式表示:AP= cm;DP= cm;BQ= cm;CQ= cm.(2)、当t为何值时,四边形APQB是平行四边形?(3)、当t为何值时,四边形PDCQ是平行四边形?25. 为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造 两种型号的沼气池共20个,以解决该村所有农户的燃料问题,两种型号沼气池的占地面积、使用农户数及造价见下表:型号
占地面积( /个)
使用农户数(户/个)
造价(万元/个)
15
18
2
20
30
3
已知可供建造沼气池的占地面积不超过 ,该村农户共有492户.
(1)、满足条件的方案共有几种?写出解答过程;(2)、通过计算判断,哪种建造方案最省钱.