江苏省南京市溧水区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-10-19 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图形中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若式子 $\frac{x - 2}{x}$ 在实数范围内有意义，则x的取值范围是（）

A、x＞0 B、x≠0 C、x ≠2 D、x≠0且x ≠2

查看试题解析
3. 下列说法中，正确的是（）

A、某种彩票中奖概率为10%是指买十张一定有一张中奖 B、“打开电视，正在播放最强大脑节目”是必然事件 C、神舟飞船发射前需要对零部件进行抽样调查 D、了解某种炮弹杀伤半径适合抽样调查

查看试题解析
4. 如图，曲线表示温度T（℃）与时间t（h）之间的函数关系，它是一个反比例函数的图象的一支.当温度T≤2℃时，时间t应（）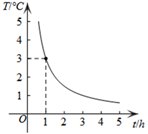

A、不小于 $\frac{2}{3}$ h B、不大于 $\frac{2}{3}$ h C、不小于 $\frac{3}{2}$ h D、不大于 $\frac{3}{2}$ h

查看试题解析
5. 在▱ABCD中，对角线AC、BD相交于点O，若∠ABC＝90°，则下列结论错误的是（）

A、AC＝BD B、OA＝OB C、AC⊥BD D、AB＝CD

查看试题解析
6. 某种植基地2018年蔬菜产量为64吨，预计2020年蔬菜产量比2019年增加20吨，求蔬菜产量的年平均增长率.设蔬菜产量的年平均增长率为x ，则下面所列的方程中正确的是（）

A、64（1＋x）²＝84 B、64（1＋x²）＝84 C、64（1＋x）x＝20 D、64（1＋x）²－64x＝20

查看试题解析

二、填空题

7. 计算：（ $\sqrt{4}$ ）²＝； $\sqrt{{(- 3)}^{2}}$ ＝.

查看试题解析
8. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
9. 计算： $\frac{x}{x - 1}$ + $\frac{1}{1 - x}$ = ．

查看试题解析
10. 计算 $\sqrt{12} \div \sqrt{3}$ =

查看试题解析
11. 已知点A（x₁ ， y₁），B（x₂ ， y₂）是反比例函数y＝ $\frac{6}{x}$ 的图像上的两点，若x₁＞x₂＞0，则y₁y₂（填“＜”、“＞”或“＝”）

查看试题解析
12. 已知x₁、x₂是方程x²－x－2＝0的两个根，则x₁＋x₂＋2x₁x₂＝.

查看试题解析
13. 如图，在▱ABCD中，AC＝BC，∠CAD＝20°，则∠D的度数为°.

查看试题解析
14. 为了改善生态环境，防止水土流失，某村计划在荒坡上种树480棵.由于青年志愿者的支援，每天比原计划多种10棵，结果提前4天完成任务.设原计划每天种x棵树，则根据题意可列方程为.

查看试题解析
15. 如图，平行于x轴的直线l与反比例函数y＝ $\frac{1}{x}$ （x＞0）和y＝ $\frac{k}{x}$ （x＞0）的图象交于A、B两点，点C是x轴上任意一点，且△ABC的面积为2，则k的值为.

查看试题解析
16. 如图，在矩形ABCD中， AB＝3，AD＝10，点E在AD上且DE＝2.点G为AE的中点，点P为BC边上的一个动点，F为EP的中点，则GF＋EF的最小值为.

查看试题解析

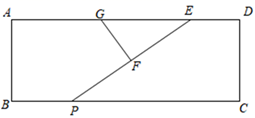
三、解答题

17. 计算 $\sqrt{5} \times (2 - \sqrt{\frac{1}{5}})$ .

查看试题解析
18. 先化简，再求值 $(\frac{1}{a - 1} - \frac{1}{a^{2} - 1}) \div \frac{a^{2} - a}{a^{2} - 1}$ ，在0、1、－1、2四个数中选一个合适的数代入求值.

查看试题解析
19. 解方程：x（x+3）=﹣2

查看试题解析
20. 解方程 $\frac{3}{x^{2} - 9} + 1 = \frac{x}{x - 3}$ .

查看试题解析
21. 某校在初二年级开设了素描、舞蹈、合唱、魔方四个社团，为了解学生最喜欢哪一个社团，随机抽取了部分学生进行调查，并将调查结果绘制成了如下两幅不完整的统计图，请根据统计图回答下列问题：

(1)、本次抽样调查的样本容量是；

(2)、请将条形统计图补充完整；

(3)、已知该校初二年级共有学生900人，根据调查结果估计该校喜欢合唱和舞蹈社团的学生共有人.

查看试题解析
22. 已知：关于x的一元二次方程x²＋mx＝3（m为常数）.

(1)、证明：无论m为何值，该方程都有两个不相等的实数根；

(2)、若方程有一个根为2，求方程的另一个根.

查看试题解析
23. 如图，经过原点的直线y₁与双曲线y₂＝ $\frac{k}{x}$ （k为常数，k≠0）交于A、B两点，其中点A的坐标为（1，2）

(1)、求k的值；

(2)、当y₁＞y₂时，请你直接写出x的取值范围.

查看试题解析
24. 已知：如图，在正方形ABCD中，点E、F在对角线AC上，且AE=CF.

(1)、求证：DE∥BF

(2)、若四边形DEBF的面积为8，AE＝ $\sqrt{2}$ ，则正方形边长为.

查看试题解析
25. 如图，有一块宽为16m的矩形荒地，某公园计划将其分为A、B、C三部分，分别种植不同的植物.若已知A、B地块为正方形，C地块的面积比B地块的面积少40m² ，试求该矩形荒地的长.

查看试题解析
26. 同学们：八年级下册第9章我们学习了一种新的图形变换旋转，图形旋转过程中蕴含着众多数学规律，以图形旋转为依托构建的解题方法是解决各类几何问题的常用方法.

(1)、（问题提出）
如图①，在正方形ABCD中，∠MAN=45°，点M、N分别在边BC、CD上.求证：MN＝BM＋DN.

证明思路如下：

第一步：如图②，将 $△ A D N$ 绕点A按顺时针方向旋转90°得到△ABE，再证明E、B、M三点在一条直线上.

第二步：证明 $△ A E M ≌ △ A N M$ .

请你按照证明思路写出完整的证明过程.

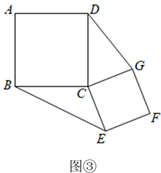
(2)、（初步思考）
如图③，四边形ABCD和CEFG为正方形，连接DG、BE，得到 $△ D C G$ 和 $△ B C E$ .

下列关于这两个三角形的结论：①周长相等； ②面积相等； ③∠CBE=∠CDG.

其中所有正确结论的序号是.

如图④，分别以▱ABCD的四条边为边向外作正方形，连接EF，GH，IJ，KL.若▱ABCD的面积为8，则图中阴影部分（四个三角形）的面积之和为.

查看试题解析