湖北省随州市随县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-10-19 类型:期末考试
一、选择题
-
1. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、2. 我市某一周每一天的最高气温统计如下表,则这组数据的中位数和众数分别是( )
最高气温(℃)
32
33
34
35
天数
1
1
2
3
A、33,34 B、34,35 C、34.5,35 D、35,353. 下列说法中错误的是( )A、在 中,若 ,则 是直角三角形 B、在 中,若 ,则 是直角三角形 C、在 中,若 , , 的度数比是7:3:4,则 是直角三角形 D、在 中,若三边长 ,则 是直角三角形4. 已知点 , ,都在直线 上,则 , 的大小关系是( )A、 B、 C、 D、无法比较5. 下列各组条件中,不能判定四边形 是平行四边形的是( )A、 , B、 , C、 , D、 ,6. 下列说法正确的是( )A、样本7,7,6,5,4的众数是2 B、样本1,2,3,4,5,6的中位数是4 C、若数据 , ,…, 的平均数是 ,则 D、样本50,50,39,41,41不存在众数7. 表示一次函数 与正比例函数 ( , 是常数且 )图象可能是( )A、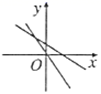 B、
B、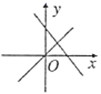 C、
C、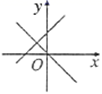 D、
D、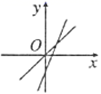 8. 下列命题中,是真命题的是( )A、四个角相等的菱形是正方形 B、有一个角是直角的四边形是矩形 C、有两边相等的平行四边形是菱形 D、两条对角线互相垂直且相等的四边形是正方形9. 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E , PF⊥AC于F , M为EF中点,则AM的最小值为( )
8. 下列命题中,是真命题的是( )A、四个角相等的菱形是正方形 B、有一个角是直角的四边形是矩形 C、有两边相等的平行四边形是菱形 D、两条对角线互相垂直且相等的四边形是正方形9. 如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E , PF⊥AC于F , M为EF中点,则AM的最小值为( ) A、 B、 C、 D、10. 如图,直线 与坐标轴相交于点 , ,将 沿直线 翻折到 的位置,当点 的坐标为 时,直线 的函数解析式是( )
A、 B、 C、 D、10. 如图,直线 与坐标轴相交于点 , ,将 沿直线 翻折到 的位置,当点 的坐标为 时,直线 的函数解析式是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 函数y= 中自变量x的取值范围是 .12. 在▱ABCD中,如果∠A+∠C=140°,那么∠B=度.13. 如图,在 中, ,如果 、 、 分别是 、 、 的中点, ,那么 .
 14. 已知数据 , ,…, 的平均数是3,方差是3,则数据 , , ,…, 的平均数是 , 方差是.15. 已知一次函数 ( 为常数,且 ).若当 时,函数有最大值7,则 的值为.16. 如图,在平面直角坐标系xOy中,菱形AOBC的边长为8,∠AOB=60°. 点D是边OB上一动点,点E在BC上,且∠DAE=60°.
14. 已知数据 , ,…, 的平均数是3,方差是3,则数据 , , ,…, 的平均数是 , 方差是.15. 已知一次函数 ( 为常数,且 ).若当 时,函数有最大值7,则 的值为.16. 如图,在平面直角坐标系xOy中,菱形AOBC的边长为8,∠AOB=60°. 点D是边OB上一动点,点E在BC上,且∠DAE=60°.
有下列结论:
①点C的坐标为(12, );②BD=CE;
③四边形ADBE的面积为定值;
④当D为OB的中点时,△DBE的面积最小.
其中正确的有.(把你认为正确结论的序号都填上)
三、解答题
-
17. 计算:(1)、 ;(2)、18. 在△ABC中,∠C=30°,AC=4cm,AB=3cm,求BC的长.
 19. 如图,直线 与y轴的交点为A,直线 与直线 的交点M的坐标为 .
19. 如图,直线 与y轴的交点为A,直线 与直线 的交点M的坐标为 .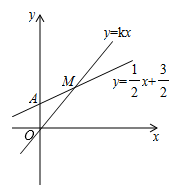 (1)、求a和k的值;(2)、直接写出关于x的不等式 的解集;(3)、若点B在x轴上, ,直接写出点B的坐标.20. 甲,乙两校的学生人数基本相同,为了解这两所学校学生的数学学业水平,在某次测试中,从两校各随机抽取了30名学生的测试成绩进行调查分析,其中甲校已经绘制好了条形统计图,乙校只完成了一部分,
(1)、求a和k的值;(2)、直接写出关于x的不等式 的解集;(3)、若点B在x轴上, ,直接写出点B的坐标.20. 甲,乙两校的学生人数基本相同,为了解这两所学校学生的数学学业水平,在某次测试中,从两校各随机抽取了30名学生的测试成绩进行调查分析,其中甲校已经绘制好了条形统计图,乙校只完成了一部分,甲校:93 82 76 77 76 89 89 89 83 87 88 89 84 92 87 89 79
54 88 92 90 87 68 76 94 84 76 69 83 92
乙校:84 63 90 89 71 92 87 92 85 61 79 91 84 92 92 73 76
92 84 57 87 89 88 94 83 85 80 94 72 90
 (1)、请根据乙校的数据补全条形统计图;(2)、两组样本数据的平均数、中位数、众数如表所示,写出 , 的值;
(1)、请根据乙校的数据补全条形统计图;(2)、两组样本数据的平均数、中位数、众数如表所示,写出 , 的值;平均数
中位数
众数
甲校
83.4
87
89
乙校
83.2
(3)、两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些,请为他们各写出一条可以使用的理由:甲校: , 乙校:.(4)、综合来看,可以推断出校学生的数学业水平更好些,理由为.21. 如图, 中, , ,且 , 是 的中点.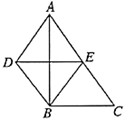 (1)、求证:四边形 是菱形.(2)、如果 , ,求四边形 的面积.(3)、当 度时,四边形 是正方形(不证明)22. 某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司62辆A,B两种型号客车作为交通工具.下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
(1)、求证:四边形 是菱形.(2)、如果 , ,求四边形 的面积.(3)、当 度时,四边形 是正方形(不证明)22. 某学校计划组织全校1441名师生到相关部门规划的林区植树,经过研究,决定租用当地租车公司62辆A,B两种型号客车作为交通工具.下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:型号
载客量
租金单价
A
30人/辆
380元/辆
B
20人/辆
280元/辆
注:载客量指的是每辆客车最多可载该校师生的人数.
(1)、设租用A型号客车x辆,租车总费用为y元,求y与x的函数表达式,并写出x的取值范围;(2)、若要使租车总费用不超过21940元,一共有几种租车方案?哪种租车方案最省钱?23. 在进行二次根式的化简时,我们有时会碰上如 , , 这样的式子,其实我们还可以将其进一步化简:①
②
③
以上这种化简的方法称之为分母有理化.
还可以用以下方法化简:
④
(1)、请你根据上面的方法化简: ; ;(2)、请参照③式,化简 ;(3)、请参照④式,化简 ;(4)、化简:24. 已知矩形 的一条边 , 是 边上的一点,将矩形 沿折痕 折叠,使得顶点 落在 边上的点 处, (如图1). (1)、求 的长(2)、擦去折痕 ,连结 ,设 是线段 上的一个动点(点 与点 , 不重合). 是 延长线上的一个动点,并且满足 ,过点 作 ,垂足为 ,连结 交 于点 (如图2).
(1)、求 的长(2)、擦去折痕 ,连结 ,设 是线段 上的一个动点(点 与点 , 不重合). 是 延长线上的一个动点,并且满足 ,过点 作 ,垂足为 ,连结 交 于点 (如图2).
①若 是 的中点,求 的长;
②试问当点 , 在移动过程中,线段 的长度是否发生变化?若变化,说明理由;若不变,求出线段 的长度.