湖北省随州市曾都区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-10-19 类型:期末考试
一、选择题
-
1. 要使代数式 有意义,则 的取值范围是A、 B、 C、 D、2. 如图,在平行四边形ABCD中,∠A=40°,则∠C大小为( )
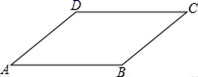 A、40° B、80° C、140° D、180°3. 下列各组数中,不能构成直角三角形的是( )A、1,1, B、13,14,15 C、 ,4,5 D、15,8,174. 关于函数 ,下列判断正确的是( )A、图象经过第一、三象限 B、 随 的增大而减小 C、图象经过点 D、无论 为何值,总有5. 如图,是某校男子足球队的年龄分布条形图,则这些队员年龄的众数为( )
A、40° B、80° C、140° D、180°3. 下列各组数中,不能构成直角三角形的是( )A、1,1, B、13,14,15 C、 ,4,5 D、15,8,174. 关于函数 ,下列判断正确的是( )A、图象经过第一、三象限 B、 随 的增大而减小 C、图象经过点 D、无论 为何值,总有5. 如图,是某校男子足球队的年龄分布条形图,则这些队员年龄的众数为( )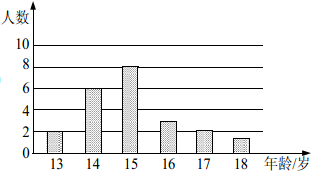 A、8 B、10 C、15 D、186. 下列等式成立的是( )A、 B、 C、 D、7. 已知直线y=kx+b不经过第一象限,则下列结论正确的是( )A、k>0,b<0 B、k<0,b<0 C、k<0,b≤0 D、k<0,b≥08. 如图,在菱形ABCD中,E,F分别是AB,AC的中点,如果EF=2,那么菱形ABCD周长是( )
A、8 B、10 C、15 D、186. 下列等式成立的是( )A、 B、 C、 D、7. 已知直线y=kx+b不经过第一象限,则下列结论正确的是( )A、k>0,b<0 B、k<0,b<0 C、k<0,b≤0 D、k<0,b≥08. 如图,在菱形ABCD中,E,F分别是AB,AC的中点,如果EF=2,那么菱形ABCD周长是( )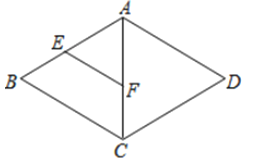 A、4 B、8 C、12 D、169. 下列说法:①对角线互相平分的四边形是平行四边形,②对角线相等且互相平分的四边形是矩形,③对角线互相垂直的四边形是菱形,④对角线互相垂直且相等的平行四边形是正方形.其中正确说法的个数为( )A、1 B、2 C、3 D、410. 为增强身体素质,小明每天早上坚持沿着小区附近的矩形公园ABCD练习跑步,爸爸站在的某一个固定点处负责进行计时指导。假设小明在矩形公园ABCD的边上沿着A→B→C→D→A的方向跑步一周,小明跑步的路程为x米,小明与爸爸之间的距离为y米.y与x之间的函数关系如图2所示,则爸爸所在的位置可能为图1的( )
A、4 B、8 C、12 D、169. 下列说法:①对角线互相平分的四边形是平行四边形,②对角线相等且互相平分的四边形是矩形,③对角线互相垂直的四边形是菱形,④对角线互相垂直且相等的平行四边形是正方形.其中正确说法的个数为( )A、1 B、2 C、3 D、410. 为增强身体素质,小明每天早上坚持沿着小区附近的矩形公园ABCD练习跑步,爸爸站在的某一个固定点处负责进行计时指导。假设小明在矩形公园ABCD的边上沿着A→B→C→D→A的方向跑步一周,小明跑步的路程为x米,小明与爸爸之间的距离为y米.y与x之间的函数关系如图2所示,则爸爸所在的位置可能为图1的( )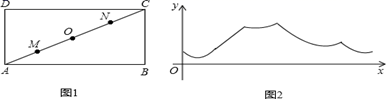 A、D点 B、M点 C、O点 D、N点
A、D点 B、M点 C、O点 D、N点二、填空题
-
11. 将二次根式 化为最简二次根式为.12. 将函数y=3x+1的图象沿y轴向下平移2个单位长度,所得直线的函数表达式为 .
13. 某公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照 的比确定.甲应试者的各项成绩如下表:应试者
听
说
读
写
甲
73
80
82
83
则甲应试者的综合成绩为.
14. 如图,在 中,按以下步骤作图: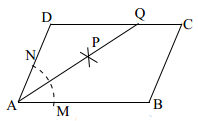
①以 为圆心,任意长为半径作弧,分别交 , 于点 , ;
②分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;
③作射线 ,交边 于点 .若 , ,则 .
15. 若直线y=kx+b(k≠0)的图象经过点(0,2),且与坐标轴所围成的三角形面积是2,则k的值为16. 数学兴趣小组开展以下折纸活动:先对折矩形 (已知 , ),使 和 重合,得到折痕 ,把纸片展平;再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 ,延长 交 于点 .同学们通过观察、探究、计算得到下列结论:① ,② 是等边三角形,③ ,④ .其中正确的结论的序号是.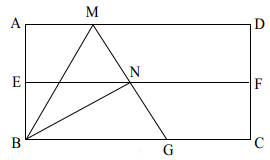
三、解答题
-
17. 计算下列各题:(1)、 ;(2)、 .18. 如图,在四边形 中, , , , , .
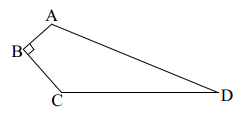 (1)、连接 ,求证: 是直角三角形;(2)、求 中 边上的高.19. 在平面直角坐标系 中,直线 与直线 交于点 ,点 在直线 上.
(1)、连接 ,求证: 是直角三角形;(2)、求 中 边上的高.19. 在平面直角坐标系 中,直线 与直线 交于点 ,点 在直线 上.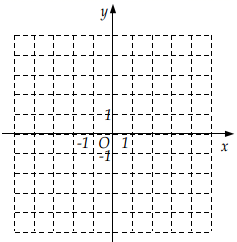 (1)、求直线 的解析式;(2)、在如图所示的坐标系中,画出直线 和 ;(3)、直接写出关于 的不等式 的解集.20. 聪聪同学要证明平行四边形的判定定理“一组对边平行且相等的四边形是平行四边形”是正确的,他先画出如图的四边形 ,并写出了如下不完整的已知和求证.
(1)、求直线 的解析式;(2)、在如图所示的坐标系中,画出直线 和 ;(3)、直接写出关于 的不等式 的解集.20. 聪聪同学要证明平行四边形的判定定理“一组对边平行且相等的四边形是平行四边形”是正确的,他先画出如图的四边形 ,并写出了如下不完整的已知和求证.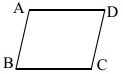
已知:如图,在四边形 中, ,________.
求证:四边形 是________四边形.
(1)、补全方框中的已知和求证,并写出证明过程;(2)、用文字叙述所证命题的逆命题.21. 甲、乙两人在 次打靶测试中命中的环数如下:甲:8,8,7,8,9
乙:5,9,7,10,9
(1)、填写下表:平均数
众数
中位数
方差
甲
8
8
乙
9
3.2
(2)、教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?(3)、如果乙再射击1次,命中8环,那么乙的射击成绩的方差是否发生变化?如果变化,会怎样变化?22. 阅读下列材料,解答后面的问题:我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积.用现代式子表示即为: ……①(其中 、 、 为三角形的三边长, 为面积).而另一个文明古国古希腊也有求三角形面积的“海伦公式”: ……②(其中 )(1)、若已知三角形的三边长分别为3,5,6,试分别运用公式①和公式②计算该三角形的面积 ;(2)、你能否由公式①推导出公式②?请试试写出推导过程.23. 已知四边形 是正方形,点 , 分别在射线 ,射线 上, , 与 交于点 .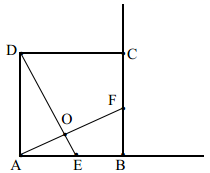
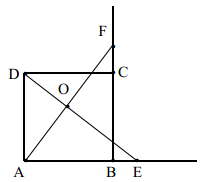
图1 图2
(1)、如图1,当点 , 分别在线段 , 上时,则线段 与线段 的数量关系是 , 位置关系是.(2)、如图2,当点 , 分别在 , 的延长线上时,将线段 沿 平移至 ,连接 , .请你补全图形,判断 的形状,并给出证明.(3)、在(2)的条件下,若正方形 的边长为3, ,请直接写出 的长.24. 某帮扶工作队将帮扶村生产的优质香菇和大米销往全国.相关信息如表:商品
规格
成本/(元/袋)
售价/(元/袋)
香菇
袋
40
60
大米
袋
38
53
已知销售表中规格的香菇和大米共1000袋,其中香菇不少于300袋,大米不少于400袋.设销售香菇 袋,销售香菇和大米获得的利润为 元.
(1)、求 (元)与 (袋)之间的函数关系式,并写出 的取值范围;(2)、销售完这批香菇和大米,至少可获得多少元的利润?(3)、因该村有部分特困户,工作队与村委会讨论决定,每销售一袋香菇提取 元作为爱心基金.如果 ,求销售完这批香菇和大米,扣除爱心基金后的最大利润(用含 的代数式表示).