湖北省黄石市大冶市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-10-19 类型:期末考试
一、选择题
-
1. 若 在实数范围内有意义,则x的取值范围是( )A、x>3 B、x>-3 C、x≥-3 D、x≤-32. 下列四组线段中,可以构成直角三角形的是( )A、1, , B、2,3,4 C、1,2,3 D、4,5,63. 某班数学兴趣小组8名同学的毕业升学体育测试成绩依次为:30,29,28,27,28,29,30,28,这组数据的众数是( )A、27 B、28 C、29 D、304. 下列各式中,一定是二次根式的是( )A、 B、 C、 D、5. 已知 ,则 的值为( )A、 B、 C、 D、06. 在平面直角坐标系中,点 关于x轴对称的点的坐标为( )A、 B、 C、 D、7. 在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )A、如果∠A﹣∠B=∠C,那么△ABC是直角三角形 B、如果a2=b2﹣c2 , 那么△ABC是直角三角形且∠C=90° C、如果∠A:∠B:∠C=1:3:2,那么△ABC是直角三角形 D、如果a2:b2:c2=9:16:25,那么△ABC是直角三角形8. 在△ABC中,AB=15,AC=13,BC上的高AD长为12,则△ABC的面积为( )A、84 B、24 C、24或84 D、42或849. 下列命题是真命题的是( )A、四条边都相等的四边形是正方形 B、四个角相等的四边形是矩形 C、平行四边形,菱形,矩形都既是轴对称图形,又是中心对称图形 D、顺次连接一个四边形四边中点得到的四边形是矩形,则原来的四边形一定是菱形10. 已知函数 的图象为“W”型,直线y=kx-k+1与函数y1的图象有三个公共点,则k的值是( )A、1或 B、0或 C、 D、 或
二、填空题
-
11. 使式子 有意义,则x的取值范围为.12. 已知P1(-3,y1)、P2(2,y2)是一次函数y=-2x+1图象上的两个点,则y1y2.13. 如图是一块地的平面示意图,已知AD=4 m,CD=3 m,AB=13 m,BC=12 m,∠ADC=90°,则这块地的面积为m2.
 14. 如图,把一张长方形纸条ABCD沿AF折叠.已知∠ADB=25°,AE∥BD,则∠BAF=.
14. 如图,把一张长方形纸条ABCD沿AF折叠.已知∠ADB=25°,AE∥BD,则∠BAF=. 15. 如图,在锐角△ABC中,AB=4 ,∠BAC=45°,∠BAC的平分线交BC于点D , M、N分别是AD和AB上的动点,则BM+MN的最小值是 .
15. 如图,在锐角△ABC中,AB=4 ,∠BAC=45°,∠BAC的平分线交BC于点D , M、N分别是AD和AB上的动点,则BM+MN的最小值是 .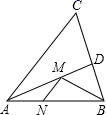 16. 正方形 , , ,…按如图所示的方式放置.点 和点 分别在直线 和x轴上,已知点 , ,则 的坐标是.
16. 正方形 , , ,…按如图所示的方式放置.点 和点 分别在直线 和x轴上,已知点 , ,则 的坐标是.
三、解答题
-
17. 计算: .18. 化简求值: ,其中 , .19. 如图,▱ABCD中,点E、F是对角线AC上的两点,且AE=CF.
求证:BF DE.
 20. 为了在甲、乙两名学生中选拔一人参加全国数学竞赛,在相同条件下,对他们进行了10次测验,成绩如下表所示:
20. 为了在甲、乙两名学生中选拔一人参加全国数学竞赛,在相同条件下,对他们进行了10次测验,成绩如下表所示:甲的成绩(分)
76
84
90
86
81
87
86
82
85
83
乙的成绩(分)
82
84
85
89
79
80
91
89
74
79
(1)、甲成绩的众数是分,乙成绩的中位数是分.(2)、若甲成绩的平均数是 甲 , 乙成绩的平均数是 乙 , 则 甲与 乙的大小关系是.(3)、经计算知: , ,这表明.(4)、若测验分数在85分(含85分)以上为优秀,则甲的优秀率为 , 乙的优秀率为21. 如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F. (1)、证明:四边形CDEF是平行四边形;(2)、若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.22. 平面直角坐标系xOy中,直线y= x+b与直线y= x交于点A(m,1).与y轴交于点B(1)、求m的值和点B的坐标;(2)、若点C在y轴上,且△ABC的面积是1,请直接写出点C的坐标.23. 小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题:
(1)、证明:四边形CDEF是平行四边形;(2)、若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.22. 平面直角坐标系xOy中,直线y= x+b与直线y= x交于点A(m,1).与y轴交于点B(1)、求m的值和点B的坐标;(2)、若点C在y轴上,且△ABC的面积是1,请直接写出点C的坐标.23. 小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题: (1)、小帅的骑车速度为千米/小时;点C的坐标为;(2)、求线段AB对应的函数表达式;(3)、当小帅到达乙地时,小泽距乙地还有多远?24. 如图,在 中,∠ACB=45°,点E在对角线AC上,BE= BA,BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连接EH.
(1)、小帅的骑车速度为千米/小时;点C的坐标为;(2)、求线段AB对应的函数表达式;(3)、当小帅到达乙地时,小泽距乙地还有多远?24. 如图,在 中,∠ACB=45°,点E在对角线AC上,BE= BA,BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连接EH. (1)、若 ,AB=13,求AF的长;(2)、连接EG,试判断 的形状,并证明你的结论.(3)、求证:EB=EH.25. 如图1,直线 分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
(1)、若 ,AB=13,求AF的长;(2)、连接EG,试判断 的形状,并证明你的结论.(3)、求证:EB=EH.25. 如图1,直线 分别与y轴、x轴交于点A、点B,点C的坐标为(-3,0),D为直线AB上一动点,连接CD交y轴于点E.
 (1)、点B的坐标为 , 不等式 的解集为(2)、若S△COE=S△ADE , 求点D的坐标;(3)、如图2,以CD为边作菱形CDFG,且∠CDF=60°.当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.
(1)、点B的坐标为 , 不等式 的解集为(2)、若S△COE=S△ADE , 求点D的坐标;(3)、如图2,以CD为边作菱形CDFG,且∠CDF=60°.当点D运动时,点G在一条定直线上运动,请求出这条定直线的解析式.