河南省周口市西华县2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-10-19 类型:期末考试
一、选择题
-
1. 要使分式 有意义, 的取值范围是( )A、 B、 C、 D、 且2. 规定 ,则 的值是( )A、 B、 C、-1 D、33. 下列叙述中,正确的是( )A、直角三角形中,两条边的平方和等于第三边的平方 B、 中, 的对边分别为 ,若 ,则 C、若 是直角三角形,且 ,则 D、若 ,则 是直角三角形4. 若一组数据 , , 的平均数为4,方差为3,那么数据 , , 的平均数和方差分别是( )A、4, 3 B、6 3 C、3 4 D、6
 5
5. 如图,长方形纸片ABCD中,点E是AD的中点,且AE=1,BE的垂直平分线MN恰好过C.则长方形的一边CD的长度为( )
5
5. 如图,长方形纸片ABCD中,点E是AD的中点,且AE=1,BE的垂直平分线MN恰好过C.则长方形的一边CD的长度为( )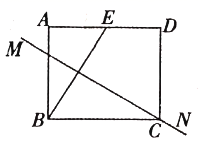 A、1 B、 C、 D、26. 如图,所有的四边形是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为13 cm,则图中所有的正方形的面积之和为( )
A、1 B、 C、 D、26. 如图,所有的四边形是正方形,所有的三角形都是直角三角形,其中最大的正方形边长为13 cm,则图中所有的正方形的面积之和为( )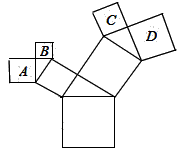 A、169cm2 B、196cm2 C、338cm2 D、507cm27. 函数 的图象是( )A、
A、169cm2 B、196cm2 C、338cm2 D、507cm27. 函数 的图象是( )A、 B、
B、 C、
C、 D、
D、 8. 已知函数 与 在同一平面直角坐标系内的图象如图所示,由图象可知, 取什么值时 ( )
8. 已知函数 与 在同一平面直角坐标系内的图象如图所示,由图象可知, 取什么值时 ( ) A、 或 B、 或 C、 或 D、 或9. 在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是( )
A、 或 B、 或 C、 或 D、 或9. 在物理实验课上,小明用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是( ) A、
A、 B、
B、 C、
C、 D、
D、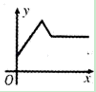 10. 已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )A、选①② B、选②③ C、选①③ D、选②④
10. 已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是( )A、选①② B、选②③ C、选①③ D、选②④二、填空题
-
11. 如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数(cm)
185
180
185
180
方差
3.6
3.6
7.4
8.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择.
12. 将一副三角尺按如图所示叠放在一起,若 ,则阴影部分的面积是 . 13. 如果一次函数 ( 是常数, )的图象过点 ,那么 的值随 的增大而(填“增大”或“减小”).14. 如图所示, 、 是四边形 的两条对角线,且 ,已知 分别是 的中点,则 .
13. 如果一次函数 ( 是常数, )的图象过点 ,那么 的值随 的增大而(填“增大”或“减小”).14. 如图所示, 、 是四边形 的两条对角线,且 ,已知 分别是 的中点,则 .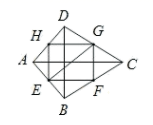 15. 如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm点E是BC边上一点,连接AE并将△AEB沿AE折叠, 得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为cm.
15. 如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm点E是BC边上一点,连接AE并将△AEB沿AE折叠, 得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为cm.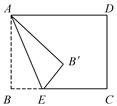
三、解答题
-
16. 计算(1)、(2)、17. 一个三角形的三边长分别为 .(1)、求它的周长(要求结果是最简二次根式);(2)、请你给出一个适当的 值,使它的周长为整数,并求出此时三角形的周长.18. 如图所示,是交警在一个路口统计的某个时段来往车辆的车速(单位: )
 (1)、交警一共统计了多少辆车?(2)、车速的众数和中位数各是多少?(3)、若该路口限速 ,即车辆超过 为超速,据统计,该路口每天来往车辆约 辆,请估计每天会有多少辆车超速?19. 如图,在▱ABCD中,已知AB>BC.
(1)、交警一共统计了多少辆车?(2)、车速的众数和中位数各是多少?(3)、若该路口限速 ,即车辆超过 为超速,据统计,该路口每天来往车辆约 辆,请估计每天会有多少辆车超速?19. 如图,在▱ABCD中,已知AB>BC.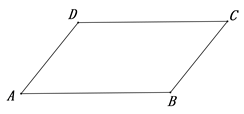 (1)、实践与操作:作∠ADC的平分线交AB于点E,在DC上截取DF=AD,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(1)、实践与操作:作∠ADC的平分线交AB于点E,在DC上截取DF=AD,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)、猜想并证明:猜想四边形AEFD的形状,并给予证明.
20. 如图所示,在 中, ,点 从点 开始沿 边向点 以 的速度运动,同时,另一点 从点 开始以 的速度沿 边向点 运动.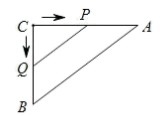 (1)、几秒钟后, 的长度是 ?(2)、几秒钟后, 的面积是 面积的 ?21. 如图,直线 与 轴交于点 ,与 轴交于点 .已知点 在直线 上,连接OC.
(1)、几秒钟后, 的长度是 ?(2)、几秒钟后, 的面积是 面积的 ?21. 如图,直线 与 轴交于点 ,与 轴交于点 .已知点 在直线 上,连接OC. (1)、求直线 的解析式;(2)、 为 轴上一动点,若 的面积是 的面积的2倍,求点 的坐标.22. 某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满.根据下表提供的信息,解答以下问题:
(1)、求直线 的解析式;(2)、 为 轴上一动点,若 的面积是 的面积的2倍,求点 的坐标.22. 某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满.根据下表提供的信息,解答以下问题:土特产种类
甲
乙
丙
每辆汽车运载量(吨)
8
6
5
每吨土特产获利(百元)
12
16
10
(1)、设装运甲种土特产的车辆数为 ,装运乙种土特产的车辆数为 ,求 与 之间的函数关系式.(2)、如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案.(3)、若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值.23. 如图 (1)、如图1所示,已知正方形 中, 是 上一点, 是 延长线上一点,且 .求证: ;(2)、如图2所示,在正方形 中, 是 上一点, 是 上一点,如果 ,请利用(1)中的结论证明: .
(1)、如图1所示,已知正方形 中, 是 上一点, 是 延长线上一点,且 .求证: ;(2)、如图2所示,在正方形 中, 是 上一点, 是 上一点,如果 ,请利用(1)中的结论证明: .