甘肃省平凉市崆峒区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-10-19 类型:期末考试
一、选择题
-
1. 函数 的自变量x的取值范围是( )A、 B、 C、 D、2. 下列根式中,是最简二次根式的是( )A、 B、 C、 D、3. 已知直角三角形的两条直角边的长分别为 和 ,则斜边的长为( )A、3 B、4 C、5 D、4. 去年某果园随机从甲、乙、丙、丁四个品种的苹果树上各采摘了15棵,四个品种的苹果树产量的平均数 (单位:千克)及方差 (单位:千克2)如表所示:
甲
乙
丙
丁
25
24
25
20
1.8
1.8
2
1.9
今年准备从四个品种中选出一种产量既高又稳定的苹果树进行种植,应选的品种是( )
A、甲 B、乙 C、丙 D、丁5. 端午节至,甲、乙两队参加了一年一度的赛龙舟比赛,两队在比赛时的路程 (米)与时间 (秒)之间的函数图象如图所示,请你根据图象判断,下列说法错误的是( ) A、甲队率先到达终点 B、甲队比乙队多走了126米 C、在47.8秒时,甲、乙两队所走的路程相等 D、乙队全程所花的时间为90.2秒6. 如图,在 中, , 分别是 、 的中点,点 在 的延长线上.添加一个条件使四边形 为平行四边形,则这个条件是( )
A、甲队率先到达终点 B、甲队比乙队多走了126米 C、在47.8秒时,甲、乙两队所走的路程相等 D、乙队全程所花的时间为90.2秒6. 如图,在 中, , 分别是 、 的中点,点 在 的延长线上.添加一个条件使四边形 为平行四边形,则这个条件是( ) A、 B、 C、 D、7. 如图,直线 与 的交点坐标为 ,则使 的 的取值范围为( )
A、 B、 C、 D、7. 如图,直线 与 的交点坐标为 ,则使 的 的取值范围为( ) A、 B、 C、 D、8. 已知某菱形的周长为 ,高为 ,则该菱形的面积为( )A、 B、 C、 D、9. 如图,在 中, , 于点 , 是 的外角的平分线, 交 于点 ,则四边形 的形状是( )
A、 B、 C、 D、8. 已知某菱形的周长为 ,高为 ,则该菱形的面积为( )A、 B、 C、 D、9. 如图,在 中, , 于点 , 是 的外角的平分线, 交 于点 ,则四边形 的形状是( )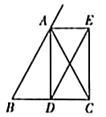 A、平行四边形 B、矩形 C、菱形 D、正方形10. 将 的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是 ,正方形 的顶点都在格点上,若直线 与正方形 有公共点,则 的值不可能是( )
A、平行四边形 B、矩形 C、菱形 D、正方形10. 将 的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是 ,正方形 的顶点都在格点上,若直线 与正方形 有公共点,则 的值不可能是( )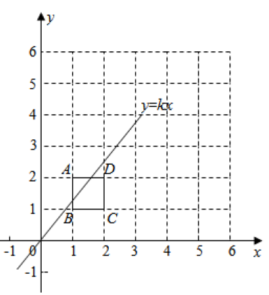 A、 B、1 C、 D、
A、 B、1 C、 D、二、填空题
-
11. 计算: .12. 数据1,2,3,4,5的平均数是.13. 若三角形的三边长满足关系式 ,则这个三角形是三角形.(填“锐角”或“直角”或“钝角”)14. 一次函数 的图象经过第一、三象限,则 的取值范围为.15. 如图,在 中, ,点 、 、 分别为 、 、 的中点,若 ,则 的长为.
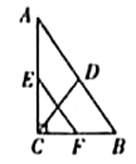 16. 在某校举行的数学竞赛中,某班10名学生的成绩统计如图所示,则这10名学生成绩的众数是分.
16. 在某校举行的数学竞赛中,某班10名学生的成绩统计如图所示,则这10名学生成绩的众数是分. 17. 在平面直角坐标系中,把直线 沿 轴向上平移后得到直线 ,如果点 是直线 上的一点,且 ,那么直线 的函数表达式为.18. 如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是.
17. 在平面直角坐标系中,把直线 沿 轴向上平移后得到直线 ,如果点 是直线 上的一点,且 ,那么直线 的函数表达式为.18. 如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是.
三、解答题
-
19. 计算:20. 计算:21. 如图,在平行四边形 中, .
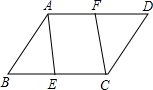
求证: .
22. 如图,直线 与直线 相交于点 . (1)、求 的值;(2)、不解关于 , 的方程组 ,请你直接写出它的解.23. 平凉市某学校进行优秀教师评比,张老师和邹老师的工作态度、教学成绩、业务学习三个方面做了一个初步统计,成绩如下:
(1)、求 的值;(2)、不解关于 , 的方程组 ,请你直接写出它的解.23. 平凉市某学校进行优秀教师评比,张老师和邹老师的工作态度、教学成绩、业务学习三个方面做了一个初步统计,成绩如下:工作态度
教学成绩
业务学习
张老师
97
95
96
邹老师
90
99
96
(1)、如果用工作态度、教学成绩、业务学习三项的平均分来计算他们的成绩,以作为评优的依据,你认为谁应被评为优秀?(2)、如果以三项成绩比例依次为20%、70%、10%来计算他们的成绩,其结果又如何?24. 如图,正方形网格中的每个小正方形的边长都是 ,每个小格的顶点叫做格点,以格点为顶点分别按下列要求作图: (1)、在图1中画一个边长为 的菱形;(2)、在图2中画一个面积为5的直角三角形.25. 如图1,某地铁车站在出入口设有上、下行自动扶梯和步行楼梯,甲、乙两人从车站入口同时下行去乘坐地铁,甲乘自动扶梯,乙走步行楼梯,乙离地铁进站入口地面的高度 (单位: )与下行时间 (单位: )之间具有函数关系 ,甲离地铁进站入口地面的高度 (单位: )与下行时间 (单位: )的函数关系如图2所示.
(1)、在图1中画一个边长为 的菱形;(2)、在图2中画一个面积为5的直角三角形.25. 如图1,某地铁车站在出入口设有上、下行自动扶梯和步行楼梯,甲、乙两人从车站入口同时下行去乘坐地铁,甲乘自动扶梯,乙走步行楼梯,乙离地铁进站入口地面的高度 (单位: )与下行时间 (单位: )之间具有函数关系 ,甲离地铁进站入口地面的高度 (单位: )与下行时间 (单位: )的函数关系如图2所示. (1)、求 关于 的函数解析式;(2)、请通过计算说明甲、乙两人谁先到达地铁进站入口地面.26. 如图1,将矩形 沿 折叠,使顶点 落在 上的点 处,然后将矩形展平.如图2,将矩形 沿 折叠,使顶点 落在折痕 上的点 处,再将矩形 沿 折叠,此时顶点 恰好落在 上的点 处.
(1)、求 关于 的函数解析式;(2)、请通过计算说明甲、乙两人谁先到达地铁进站入口地面.26. 如图1,将矩形 沿 折叠,使顶点 落在 上的点 处,然后将矩形展平.如图2,将矩形 沿 折叠,使顶点 落在折痕 上的点 处,再将矩形 沿 折叠,此时顶点 恰好落在 上的点 处.
求证:
27. 为了从甲、乙两名选手中选拔一名参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下甲、乙两人射击成绩的折线图: (1)、求甲、乙两人射击成绩的中位数;(2)、如果规定成绩较稳定者胜出,你认为谁应胜出?请通过计算方差说明理由.28. 在六一儿童节到来之际,某校特举行书画大赛活动,准备购买甲、乙两种文具作为奖品,奖励在活动中获得优秀的同学.已知购买2个甲种文具、3个乙种文具共需花费45元;购买3个甲种文具、1个乙种文具共需花费50元.(1)、问:购买一个甲种文具、一个乙种文具各需多少元?(2)、若学校计划购买这两种文具共100个,投入资金不少于995元又不多于1050元,设购买甲种文具 个,则有多少种购买方案?(3)、设学校投入资金 元,在(2)的条件下,哪种购买方需要的资金最少?最少是多少元?
(1)、求甲、乙两人射击成绩的中位数;(2)、如果规定成绩较稳定者胜出,你认为谁应胜出?请通过计算方差说明理由.28. 在六一儿童节到来之际,某校特举行书画大赛活动,准备购买甲、乙两种文具作为奖品,奖励在活动中获得优秀的同学.已知购买2个甲种文具、3个乙种文具共需花费45元;购买3个甲种文具、1个乙种文具共需花费50元.(1)、问:购买一个甲种文具、一个乙种文具各需多少元?(2)、若学校计划购买这两种文具共100个,投入资金不少于995元又不多于1050元,设购买甲种文具 个,则有多少种购买方案?(3)、设学校投入资金 元,在(2)的条件下,哪种购买方需要的资金最少?最少是多少元?