初中数学中考复习专题试卷1:最短距离问题
试卷更新日期:2020-10-19 类型:二轮复习
一、单选题
-
1. 如图,开口玻璃罐长、宽、高分别为16、6和6,在罐內点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外长方形ABCD的中心H处,蚂蚁到达饼干的最短距离是多少( )
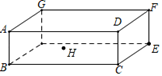 A、 B、17 C、 D、2.
A、 B、17 C、 D、2.如图,一圆柱高8cm,底面半径为cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是( )
 A、6cm B、8cm C、10cm D、12cm3. 如图,已知⊙O的半径为R,C、D在直径AB的同侧半圆上,∠AOC=96°,∠BOD=36°,动点P在直径AB上,则CP+PD的最小值是( )
A、6cm B、8cm C、10cm D、12cm3. 如图,已知⊙O的半径为R,C、D在直径AB的同侧半圆上,∠AOC=96°,∠BOD=36°,动点P在直径AB上,则CP+PD的最小值是( )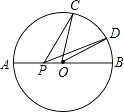 A、2R B、 R C、 R D、R4. 已知A为⊙O外一点,若点A到⊙O上的点的最短距离为2,最长离为4,则⊙O半径为( )A、4 B、3 C、2 D、15. 如图,在平面直角坐标系中,点P是以C(﹣ , )为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是( )
A、2R B、 R C、 R D、R4. 已知A为⊙O外一点,若点A到⊙O上的点的最短距离为2,最长离为4,则⊙O半径为( )A、4 B、3 C、2 D、15. 如图,在平面直角坐标系中,点P是以C(﹣ , )为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是( )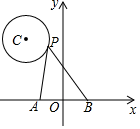 A、6 B、8 C、10 D、126. 一个钢管放在V形架内,如图是其截面图,测得P点与钢管的最短距离PB=25cm,最长距离PA=75cm.若钢管的厚度忽略不计,则劣弧 的长为( )
A、6 B、8 C、10 D、126. 一个钢管放在V形架内,如图是其截面图,测得P点与钢管的最短距离PB=25cm,最长距离PA=75cm.若钢管的厚度忽略不计,则劣弧 的长为( )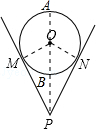 A、 πcm B、50πcm C、 πcm D、50 πcm7. 如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是( )
A、 πcm B、50πcm C、 πcm D、50 πcm7. 如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=2,ON=6,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是( )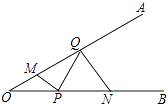 A、2 B、 C、20 D、28. 如图,△ABC中,AC=3,BC= ,∠ACB=60°,过点A作BC的平行线l,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则AE的最小值为( )
A、2 B、 C、20 D、28. 如图,△ABC中,AC=3,BC= ,∠ACB=60°,过点A作BC的平行线l,P为直线l上一动点,⊙O为△APC的外接圆,直线BP交⊙O于E点,则AE的最小值为( ) A、 -1 B、7-4 C、 D、19. 如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB= .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
A、 -1 B、7-4 C、 D、19. 如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB= .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( ) A、6 B、8 C、10 D、1210. 如图,已知 , 为线段 上的一个动点,分别以 , 为边在 的同侧作菱形 和菱形 ,点 , , 在一条直线上, . , 分别是对角线 , 的中点.当点 在线段 上移动时,点 , 之间的距离最短为( )
A、6 B、8 C、10 D、1210. 如图,已知 , 为线段 上的一个动点,分别以 , 为边在 的同侧作菱形 和菱形 ,点 , , 在一条直线上, . , 分别是对角线 , 的中点.当点 在线段 上移动时,点 , 之间的距离最短为( )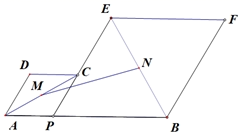 A、 B、 C、4 D、311. 已知,平面直角坐标系中,直线y1=x+3与抛物线y=- 的图象如图,点P是y2上的一个动点,则点P到直线y1的最短距离为( )
A、 B、 C、4 D、311. 已知,平面直角坐标系中,直线y1=x+3与抛物线y=- 的图象如图,点P是y2上的一个动点,则点P到直线y1的最短距离为( )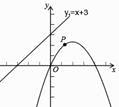 A、 B、 C、 D、12. 如图,从A到B有三条路径,最短的路径是②,理由是( )
A、 B、 C、 D、12. 如图,从A到B有三条路径,最短的路径是②,理由是( )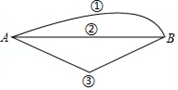 A、两点确定一条直线 B、两点之间线段最短 C、过一点有无数条直线 D、直线比曲线和折线短13. 如图,连接直线 外一点 与直线 上各点 , ,其中 ,这些线段 , , , , 中,最短的线段是( )
A、两点确定一条直线 B、两点之间线段最短 C、过一点有无数条直线 D、直线比曲线和折线短13. 如图,连接直线 外一点 与直线 上各点 , ,其中 ,这些线段 , , , , 中,最短的线段是( ) A、 B、 C、 D、14. 如图,从直线 外一点 向 引四条线段 , , , ,其中最短的一条是( )
A、 B、 C、 D、14. 如图,从直线 外一点 向 引四条线段 , , , ,其中最短的一条是( )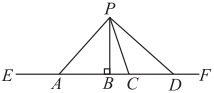 A、 B、 C、 D、15. 已知菱形 在平面直角坐标系的位置如图所示,顶点 , ,点P是对角线 上的一个动点 ,当 最短时,点P的坐标为( )
A、 B、 C、 D、15. 已知菱形 在平面直角坐标系的位置如图所示,顶点 , ,点P是对角线 上的一个动点 ,当 最短时,点P的坐标为( )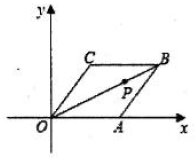 A、 B、 C、 D、16. 如图,正方体的棱长为6cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是( )
A、 B、 C、 D、16. 如图,正方体的棱长为6cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是( )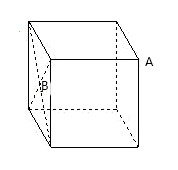 A、9 B、 C、 D、12
A、9 B、 C、 D、12二、填空题
-
17. 如图,已知∠ACB=90°,BC=6,AC=8,AB=10,点D在线段AB上运动,线段CD的最短距离是 .
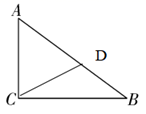 18. 如图,长方体的长为15,宽为10,高为20,点B与点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是。
18. 如图,长方体的长为15,宽为10,高为20,点B与点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是。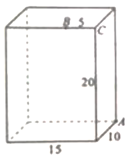 19. 菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点E坐标为(0,﹣ ),点P是对角线OC上一个动点,则EP+BP最短的最短距离为.
19. 菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点E坐标为(0,﹣ ),点P是对角线OC上一个动点,则EP+BP最短的最短距离为. 20.
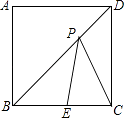
20.在正方形ABCD中,E在BC上,BE=2,CE=1,P在BD上,则PE和PC的长度之和最小可达到 .
 21. 如图,已知▱ABCO的顶点A、C分别在直线x=2和x=7上,O是坐标原点,则对角线OB长的最小值为.
21. 如图,已知▱ABCO的顶点A、C分别在直线x=2和x=7上,O是坐标原点,则对角线OB长的最小值为.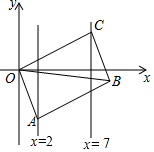 22. 四边形ABCD中,∠BAD=125°,∠B=∠D=90°,在BC、CD上分别找一点M、N,当三角形AMN周长最小时,∠MAN的度数为 .
22. 四边形ABCD中,∠BAD=125°,∠B=∠D=90°,在BC、CD上分别找一点M、N,当三角形AMN周长最小时,∠MAN的度数为 .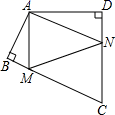 23. 如图,直线AB的解析式y= x+3,交x轴于点A,交y轴于点B,点P为线段AB上一个动点,作PE⊥x轴于点E,PF⊥y轴于点F,则线段EF的最短长度为。
23. 如图,直线AB的解析式y= x+3,交x轴于点A,交y轴于点B,点P为线段AB上一个动点,作PE⊥x轴于点E,PF⊥y轴于点F,则线段EF的最短长度为。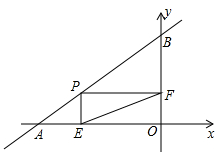 24. 如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC= ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为 .
24. 如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC= ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为 .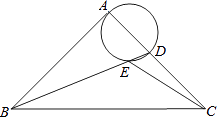 25. 如图,菱形OABC中,点A在x轴上,顶点C的坐标为(1, ),动点D、E分别在射线OC、OB上,则CE+DE+DB的最小值是.
25. 如图,菱形OABC中,点A在x轴上,顶点C的坐标为(1, ),动点D、E分别在射线OC、OB上,则CE+DE+DB的最小值是.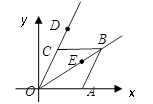 26. 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为。
26. 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动,过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为。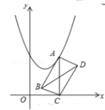 27. 如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为4cm的等边三角形 ,点 是母线 的中点,一只蚂蚁从点 出发沿圆锥的表面爬行到点 处,则这只蚂蚁爬行的最短距离是cm.
27. 如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为4cm的等边三角形 ,点 是母线 的中点,一只蚂蚁从点 出发沿圆锥的表面爬行到点 处,则这只蚂蚁爬行的最短距离是cm.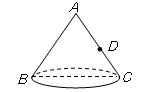 28.
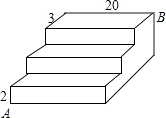
28.如图,台阶A处的蚂蚁要爬到B处搬运食物,它爬的最短距离是 .
 29. 如图,某货船以24海里/时的速度从A处向正东方向的D处航行,在点A处测得某岛C在北偏东60°的方向.该货船航行30分钟后到达B处,此时测得该岛在北偏东30°的方向上.则货船在航行中离小岛C的最短距离是 .
29. 如图,某货船以24海里/时的速度从A处向正东方向的D处航行,在点A处测得某岛C在北偏东60°的方向.该货船航行30分钟后到达B处,此时测得该岛在北偏东30°的方向上.则货船在航行中离小岛C的最短距离是 .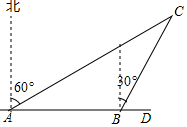 30. 如图,已知 ,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE.点P,C,E在一条直线上, ,M、N分别是对角线AC、BE的中点.当点P在线段AB上移动时,点M、N之间的距离最短为.
30. 如图,已知 ,P为线段AB上的一个动点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE.点P,C,E在一条直线上, ,M、N分别是对角线AC、BE的中点.当点P在线段AB上移动时,点M、N之间的距离最短为.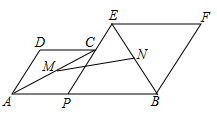 31. 在菱形 中, ,点 是 的中点, 是对角线 上的一个动点,则 的最小值为 .
31. 在菱形 中, ,点 是 的中点, 是对角线 上的一个动点,则 的最小值为 .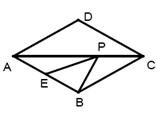 32. 如图,矩形ABCD中,AD=12,AB=8,E是AB上一点,且EB=3,F是BC上一动点,若将 沿EF对折后,点B落在点P处,则点P到点D的最短距为 .
32. 如图,矩形ABCD中,AD=12,AB=8,E是AB上一点,且EB=3,F是BC上一动点,若将 沿EF对折后,点B落在点P处,则点P到点D的最短距为 .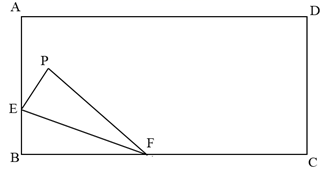
三、作图题
-
33. 尺规作图:(不要求写作法,只保留作图痕迹)
如图,工厂A和工厂B,位于两条公路OC、OD之间的地带,现要建一座货物中转站P.若要求中转站P到两条公路OC、OD的距离相等,且到工厂A和工厂B的距离之和最短,请用尺规作出P的位置.
 34. 有一个养鱼专业户,在如图所示地形的两个池塘里养鱼,他每天早上要从住处P分别前往两个池塘投放鱼食,试问他怎样走才能以最短距离回到住地?(请用尺规作图,保留作图痕迹,不写做法)
34. 有一个养鱼专业户,在如图所示地形的两个池塘里养鱼,他每天早上要从住处P分别前往两个池塘投放鱼食,试问他怎样走才能以最短距离回到住地?(请用尺规作图,保留作图痕迹,不写做法) 35. 最短路径问题:
35. 最短路径问题:例:如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短.
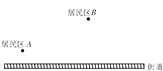
解:只有A、C、B在一直线上时,才能使AC+BC最小.作点A关于直线“街道”的对称点A′,然后连接A′B,交“街道”于点C,则点C就是所求的点.

应用:已知:如图A是锐角∠MON内部任意一点,
在∠MON的两边OM,ON上各取一点B,C,组成三角形,使三角形周长最小.
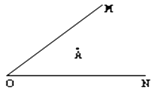 (1)、借助直角三角板在下图中找出符合条件的点B和C.(2)、若∠MON=30°,OA=10,求三角形的最小周长。
(1)、借助直角三角板在下图中找出符合条件的点B和C.(2)、若∠MON=30°,OA=10,求三角形的最小周长。四、综合题
-
36.
 (1)、(问题解决)已知点P在内,过点p分别作关于OA、OB的对称点p1、p2
(1)、(问题解决)已知点P在内,过点p分别作关于OA、OB的对称点p1、p2①如图1,若,请直接写出_▲_;
②如图2,连接p1p2分别交OA、OB于C、D,若,求的度数;
③在②的条件下,若度90<a<180),请直接写出_▲_度(用含a的代数式表示).
(2)、(拓展延伸)利用“有一个角是 的等腰三角形是等边三角形”这个结论,解答问题:如图3,在∆ABC中,点p是∆ABC内部一定点,AP=8,点E、F分别在边AB、AC上,请你在图3中画出使∆PEF周长最小的点E、F的位置(不写画法),并直接写出∆PEF周长的最小值. 37. 数学上称“费马点”是位于三角形内且到三角形三个顶点距离之和最短的点。
的等腰三角形是等边三角形”这个结论,解答问题:如图3,在∆ABC中,点p是∆ABC内部一定点,AP=8,点E、F分别在边AB、AC上,请你在图3中画出使∆PEF周长最小的点E、F的位置(不写画法),并直接写出∆PEF周长的最小值. 37. 数学上称“费马点”是位于三角形内且到三角形三个顶点距离之和最短的点。现定义:菱形对角线上一点到该对角线同侧两条边上的两点距离最小的点称为类费马点。
例如:菱形ABCD,P是对角线BD上一点,E、F是边BC和CD上的两点,若点P满足PE与PF之和最小,则称点P为类费马点
 (1)、如图1,在菱形ABCD中,AB=4,点P是BD上的类费马点
(1)、如图1,在菱形ABCD中,AB=4,点P是BD上的类费马点①E为BC的中点,F为CD的中点,则PE+PF=。
②E为BC上一动点,F为CD上一动点,且∠ABC=60°则PE+PF=。
(2)、如图2,在菱形ABCD中,AB=4,连结AC,点P是△ABC的费马点,(即PA,PB,PC之和最小),①当∠ABC=60°时,BP=▲②当∠ABC=30°时,你能找到△ABC的费马点P吗?画图做简要说明,并求此时PA+PB+PC的值
38.问题情境:如图①,P是⊙O外的一点,直线PO分别交⊙O于点A、B,可以发现PA是点P到⊙O上的点的最短距离.
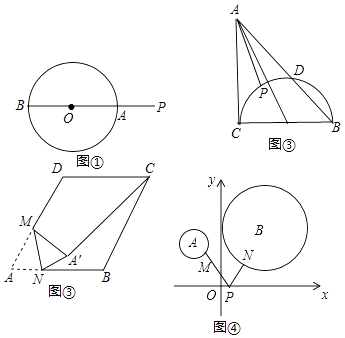 (1)、直接运用:如图②,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是弧CD上的一个动点,连接AP,则AP的最小值是 .(2)、构造运用:如图③,在边长为8的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′C长度的最小值.(3)、综合运用:如图④,平面直角坐标系中,分别以点A(﹣2,3),B(3,4)为圆心,分别以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于 .39. 请阅读下列材料
(1)、直接运用:如图②,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是弧CD上的一个动点,连接AP,则AP的最小值是 .(2)、构造运用:如图③,在边长为8的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′C长度的最小值.(3)、综合运用:如图④,平面直角坐标系中,分别以点A(﹣2,3),B(3,4)为圆心,分别以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于 .39. 请阅读下列材料问题:如图1,点A、B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小,小明的思路是:如图2所示,先作点A关于直线l的对称点A',使点A'、B分别位于直线l的两侧,再连接A'B,根据“两点间线段最短”可知A'B与直线l的交点P即为所求.
 (1)、如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D,若CP=1,AC=1,PD=2,求出AP+BP的值:(2)、将(1)中的条件“AC=1”去掉,换成“BD=4-AC”,其它条件不变,直接写出此时AP+BP的值:(3)、请结合图形,求 的最小值.
(1)、如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D,若CP=1,AC=1,PD=2,求出AP+BP的值:(2)、将(1)中的条件“AC=1”去掉,换成“BD=4-AC”,其它条件不变,直接写出此时AP+BP的值:(3)、请结合图形,求 的最小值.