初中数学浙教版2020-2021学年九年级上学期期中模拟试卷(1)
试卷更新日期:2020-10-18 类型:期中考试
一、单选题
-
1. 已知二次函数 ,则下列关于这个函数图象和性质的说法,正确的是( )A、图象的开口向上 B、图象的顶点坐标是 C、当 时,y随x的增大而增大 D、图象与x轴有唯一交点2. 下列说法中不正确的是( )A、抛掷一枚硬币,硬币落地时正面朝上是随机事件 B、把4个球放入三个抽屉中,其中一个抽屉中至少有2个球是必然事件 C、任意打开九年级上册数学教科书,正好是56页是确定事件 D、一只盒子中有白球m个,红球5个,黑球n个(每个球了颜色外都相同).如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m与n的和是53. 如图,点A,B,C,D在⊙O上, ,点B是弧AC的中点,则 的度数是( )
 A、30° B、40° C、50° D、60°4. 抛物线y=ax2+2ax+a2+2的一部分如图所示,那么该抛物线在y轴右侧与x轴交点的坐标是( )
A、30° B、40° C、50° D、60°4. 抛物线y=ax2+2ax+a2+2的一部分如图所示,那么该抛物线在y轴右侧与x轴交点的坐标是( )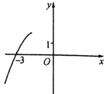 A、(0,0) B、(1,0) C、(2,0) D、(3,0)5. 为了解某地区九年级男生的身高情况,随机抽取了该地区1000名九年级男生的身高数据,统计结果如下.
A、(0,0) B、(1,0) C、(2,0) D、(3,0)5. 为了解某地区九年级男生的身高情况,随机抽取了该地区1000名九年级男生的身高数据,统计结果如下.身高
人数
60
260
550
130
根据以上统计结果,随机抽取该地区一名九年级男生,估计他的身高不低于 的概率是( )
A、0.32 B、0.55 C、0.68 D、0.876. 将抛物线 向左平移3个单位长度,再向下平移2个单位长度,得到抛物线的解析式是( )A、 B、 C、 D、7. 如图,AB为⊙O的直径,点C,点D是⊙O上的两点,连接CA,CD,AD.若∠CAB=40°,则∠ADC的度数是( )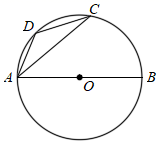 A、110° B、130° C、140° D、160°8. 已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则( )A、y3<y2<y1 B、y3<y1<y2 C、y2<y3<y1 D、y1<y3<y29. 已知锐角∠AOB如图,
A、110° B、130° C、140° D、160°8. 已知(-3,y1),(-2,y2),(1,y3)是抛物线y=-3x2-12x+m上的点,则( )A、y3<y2<y1 B、y3<y1<y2 C、y2<y3<y1 D、y1<y3<y29. 已知锐角∠AOB如图,⑴在射线OA上取一点C,以点O为圆心,OC长为半径作 ,交射线OB于点D,连接CD;
⑵分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;
⑶连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )
 A、∠COM=∠COD B、若OM=MN,则∠AOB=20° C、MN∥CD D、MN=3CD10. 如图,直线 交x轴、y轴于A、B两点,点P为线段AB上的点,过点P作 轴于点E,作 轴于点F, ,将线段AB沿y轴负方向向下移动a个单位,线段 扫过矩形 的面积为Z,则下图描述Z与a的函数图象可能是( )
A、∠COM=∠COD B、若OM=MN,则∠AOB=20° C、MN∥CD D、MN=3CD10. 如图,直线 交x轴、y轴于A、B两点,点P为线段AB上的点,过点P作 轴于点E,作 轴于点F, ,将线段AB沿y轴负方向向下移动a个单位,线段 扫过矩形 的面积为Z,则下图描述Z与a的函数图象可能是( )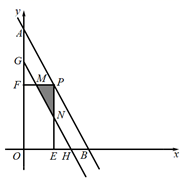 A、
A、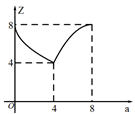 B、
B、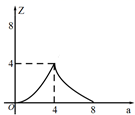 C、
C、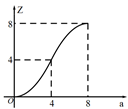 D、
D、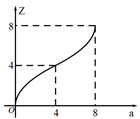
二、填空题
-
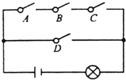
11. 若抛物线 的对称轴是y轴,则 .12. 如果正多边形的边数是n(n≥3),它的中心角是 °,那么 关于n的函数解析式是13. 二次函数y=a(x+1)(x-4)的对称轴是直线.14. 如图,电路图上有四个开关A、B、C、D和一个小灯泡,在开关全部断开的情况下,闭合其中任意一个开关,灯泡发亮的概率是;若闭合其中任意两个开关,灯泡发亮的概率是.
 15. 我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深 寸,锯道长 尺(1尺=10寸).问这根圆形木材的直径是寸.
15. 我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深 寸,锯道长 尺(1尺=10寸).问这根圆形木材的直径是寸.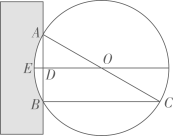 16. 如图,点A是抛物线y=x2-4x对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为 .
16. 如图,点A是抛物线y=x2-4x对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO′,当O′恰好落在抛物线上时,点A的坐标为 .
三、综合题
-
17. 如图,AB是⊙O的直径,AC是弦,OD⊥AB交AC于点D . 若∠A=30°,OD=2.求CD的长.
 18. 已知:抛物线y=﹣x2+bx+c经过点B(﹣1,0)和点C(2,3).(1)、求此抛物线的表达式;(2)、如果此抛物线沿y轴平移一次后过点(﹣2,1),试确定这次平移的方向和距离.19. 如图,已知 是 的直径, , 是 上的点, ,交 于点 ,连结 .
18. 已知:抛物线y=﹣x2+bx+c经过点B(﹣1,0)和点C(2,3).(1)、求此抛物线的表达式;(2)、如果此抛物线沿y轴平移一次后过点(﹣2,1),试确定这次平移的方向和距离.19. 如图,已知 是 的直径, , 是 上的点, ,交 于点 ,连结 .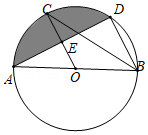 (1)、求证: ;(2)、若 , ,求图中阴影部分的面积.20. “互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,每月可多销售5条,设每条裤子的售价为x元(x为正整数),每月的销售量为y条.(1)、直接写出y与x的函数关系式;(2)、设该网店每月获得的利润为w元,当售价为多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生,为了保证捐款后每月利润为4175元,且让消费者得到最大的实惠,休闲裤的销售单价定为多少?21. 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C , 请在网格中进行下列操作:
(1)、求证: ;(2)、若 , ,求图中阴影部分的面积.20. “互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,每月可多销售5条,设每条裤子的售价为x元(x为正整数),每月的销售量为y条.(1)、直接写出y与x的函数关系式;(2)、设该网店每月获得的利润为w元,当售价为多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生,为了保证捐款后每月利润为4175元,且让消费者得到最大的实惠,休闲裤的销售单价定为多少?21. 如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C , 请在网格中进行下列操作: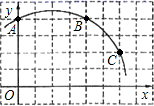 (1)、在图中确定该圆弧所在圆的圆心D点的位置,并写出点D点坐标为 .(2)、连接AD、CD , 求⊙D的半径及 的长;(3)、有一点E(6,0),判断点E与⊙D的位置关系.22. 北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共“金山银山,不如绿水青山”.某市不断推进“森林城市”建设,今春种植四类树苗,园林部门从种植的这批树苗中随机抽取了4000棵,将各类树苗的种植棵数绘制成扇形统计图,将各类树苗的成活棵数绘制成条形统计图,经统计松树和杨树的成活率较高,且杨树的成活率为97%,根据图表中的信息解答下列问题:
(1)、在图中确定该圆弧所在圆的圆心D点的位置,并写出点D点坐标为 .(2)、连接AD、CD , 求⊙D的半径及 的长;(3)、有一点E(6,0),判断点E与⊙D的位置关系.22. 北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共“金山银山,不如绿水青山”.某市不断推进“森林城市”建设,今春种植四类树苗,园林部门从种植的这批树苗中随机抽取了4000棵,将各类树苗的种植棵数绘制成扇形统计图,将各类树苗的成活棵数绘制成条形统计图,经统计松树和杨树的成活率较高,且杨树的成活率为97%,根据图表中的信息解答下列问题: (1)、扇形统计图中松树所对的圆心角为度,并补全条形统计图.(2)、该市今年共种树16万棵,成活了约多少棵?(3)、园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用A,B,C,D表示)23. “阳光体育活动”促进了学校体育活动的开展,小杰在一次铅球比赛中,铅球出手以后的轨迹是抛物线的一部分(如图所示),已知铅球出手时离地面1.6米,铅球离投掷点3米时达到最高点,在离投掷点8米处落地,
(1)、扇形统计图中松树所对的圆心角为度,并补全条形统计图.(2)、该市今年共种树16万棵,成活了约多少棵?(3)、园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用A,B,C,D表示)23. “阳光体育活动”促进了学校体育活动的开展,小杰在一次铅球比赛中,铅球出手以后的轨迹是抛物线的一部分(如图所示),已知铅球出手时离地面1.6米,铅球离投掷点3米时达到最高点,在离投掷点8米处落地, (1)、请求出此轨迹所在抛物线的关系式.(2)、设抛物线与X轴另一个交点是E,点Q是对称轴上的一个动点,求当△EBQ的周长最短时点Q的坐标。(3)、在抛物线上是否存在点G使得S△DEG=19.5,若存在请求出点G的坐标,若不存在,请说明理由.24.
(1)、请求出此轨迹所在抛物线的关系式.(2)、设抛物线与X轴另一个交点是E,点Q是对称轴上的一个动点,求当△EBQ的周长最短时点Q的坐标。(3)、在抛物线上是否存在点G使得S△DEG=19.5,若存在请求出点G的坐标,若不存在,请说明理由.24.
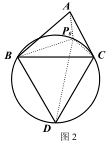
 (1)、知识储备
(1)、知识储备①如图 1,已知点 P 为等边△ABC 外接圆的弧BC 上任意一点.求证:PB+PC= PA.
②定义:在△ABC 所在平面上存在一点 P,使它到三角形三顶点的距离之和最小,则称点 P 为△ABC的费马点,此时 PA+PB+PC 的值为△ABC 的费马距离.
(2)、知识迁移①我们有如下探寻△ABC (其中∠A,∠B,∠C 均小于 120°)的费马点和费马距离的方法:
如图 2,在△ABC 的外部以 BC 为边长作等边△BCD 及其外接圆,根据(1)的结论,易知线段▲ 的长度即为△ABC 的费马距离.
②在图 3 中,用不同于图 2 的方法作出△ABC 的费马点 P(要求尺规作图).
(3)、知识应用①判断题(正确的打√,错误的打×):
ⅰ.任意三角形的费马点有且只有一个( );
ⅱ.任意三角形的费马点一定在三角形的内部( ).
②已知正方形 ABCD,P 是正方形内部一点,且 PA+PB+PC 的最小值为 ,求正方形 ABCD 的
边长.