初中数学浙教版2020-2021学年八年级上学期期中模拟试卷（2）
试卷更新日期：2020-10-18 类型：期中考试
一、单选题
-
1. 下列交通路口分流图案中，属于轴对称图形的是（ ）A、
B、
C、
D、
2. 在△ABC中，已知AB=4cm，BC=9cm，则AC的长可能是（ ）A、5cm B、12 cm C、13cm D、16cm3. 如图，已知∠AOB＝10°，且OC＝CD＝DE＝EF＝FG＝GH，则∠BGH＝ （ ）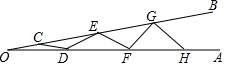
A、50° B、60° C、70° D、80°4. 如图，点E，点F在直线AC上， AE＝CF， AD＝CB，下列条件中不能判断△ADF≌△CBE的是（ ）
A、AD//BC B、BE//DF C、BE＝DF D、∠A＝∠C5. 我国古代数学著作《九章算术》中有一个问题，原文是：今有池方一丈，葭生其中央，出水一 尺，引葭赴岸，适与岸齐，问葭长几何．翻译成数学问题是：如图，有一个水池，水面是边长为 10尺的正方形，在水池的正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边，它的顶端恰好到达池边的水面，则这根芦苇的长度是（ ）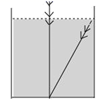
A、10尺 B、11尺 C、12尺 D、13尺6. 如图，在 中，点 是边 、 的垂直平分线的交点，已知 ，则 （ ）
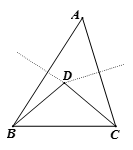A、 B、 C、 D、7. 如图，△ABC 的三边 AB、BC、CA 长分别是 10、15、20， 其三条角平分线将△ABC 分为三个三角形，则 S△ABO：S△BCO： S△CAO 等于（ ）
A、1∶1∶1 B、1∶2∶3 C、2∶3∶4 D、3∶4∶58. 下列句子中，不属于命题的是（ ）A、正数大于一切负数吗? B、两点之间线段最短 C、
不是无理数
D、会飞的动物只有鸟
9. 如图，三条公路把A，B，C三个村庄连成一个三角形区域，政府决定在这个三角形区域内修建一个集贸市场，使集贸市场到三条公路的距离相等，则该集贸市场应建在（ ）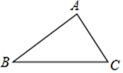
A、AC，BC两边高线的交点处 B、AC，BC两边中线的交点处 C、AC，BC两边垂直平分线的交点处 D、 ， 两内角平分线的交点处10. 如图，在Rt△ABC中，∠CBA=90°，∠CAB的角平分线AP和∠ACB外角的平分线CF相交于点D，AD交CB于点P，CF交AB的延长线于点F，过点D作DE⊥CF交CB的延长线于点G，交AB的延长线于点E，连接CE并延长交FG于点H，则下列结论：①∠CDA=45°；②AF-CG=CA；③DE=DC；④FH=CD+GH；⑤CF=2CD+EG．其中正确的有（ ）
A、①②④ B、①②③ C、①②④⑤ D、①②③⑤二、填空题
-
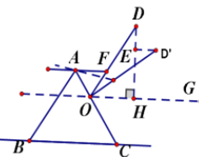
11. 平面内点A（﹣1，2）和点B（﹣1，a）关于直线y＝4对称，a＝ ．12. 已知等腰三角形一边长为3，另一边长为7，则这个等腰三角形的周长为。13. 图 1 是小红在“淘宝 双 11”活动中所购买的一张多档位可调节靠椅，档位调节示意图如图 2 所示。已知两支脚 AB=AC，O 为 AC 上固定连接点，靠背 OD=10 分米。档位为Ⅰ档时，OD∥AB，档位为Ⅱ挡时，OD’⊥AC，过点O作OG∥BC，则∠DOG+∠D’OG=°当靠椅由Ⅰ档调节为Ⅱ档时，靠背顶端 D 向后靠至 D’，此时点 D 移动的水平距离是 2 分米，即 ED’=2 分米。DH⊥OG于点H，则D到直线OG的距离为 分米。
14. 把命题“对顶角相等”改为“如果…那么…”的形式 ．15. 如图，在△ABC中，AB=AC，D、E是△ABC内两点，AD平分∠BAC，∠EBC=∠E=60°，若BE=6cm，DE=2cm，则BC=cm．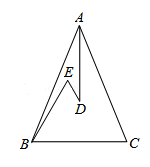
16. 如图，点P是∠AOB内任意一点，OP＝8，M、N分别是射线OA和OB上的动点，若△PMN周长的最小值为8，则∠AOB＝.
三、解答题
-
17. 如图，△ABC中，∠CAB的平分线与BC的垂直平分线DG相交于D，过点D作DE⊥AB，DF⊥AC，求证：BE＝CF．
18. 已知：如图，AB=AC，D是AB上一点，DE⊥BC于点E，ED的延长线交CA的延长线于点F.求证：△ADF是等腰三角形.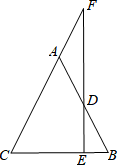
19. 如图，在△ABC中，AD平分∠BAC，且点D是BC的中点.试判断AD与BC的位置关系，并说明理由.
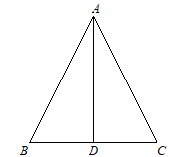20. 已知如图①，BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线，BQ、CQ分别是∠PBC、∠PCB的角平分线，BM、CN分别是∠PBD、∠PCE的角平分线，∠BAC＝α.
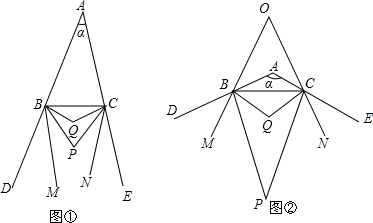(1)、当α＝40°时，∠BPC＝°，∠BQC＝°；(2)、当α＝°时，BM∥CN；(3)、如图②，当α＝120°时，BM、CN所在直线交于点O，求∠BOC的度数；(4)、在α＞60°的条件下，直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系：.21. 如图（1）、（2）所示，方格图中每个小正方形的边长为1，点A、B、C都是格点.
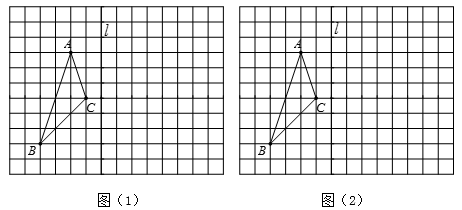(1)、在（1）画中出△ABC关于直线l对称的 ；(2)、求出图（1）中 的面积；(3)、如图(2)所示，A、C是直线l同侧固定的点，P是直线l上的一个动点，在图（2）中的直线l上画出点P，使AP+PC的值最小.22. 如图，在等边 中，点 、点 分别在 、 上， ，连接 、 交于点 ，作 于 .
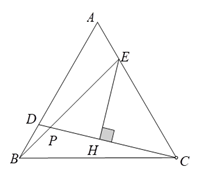(1)、求证： .(2)、求证： .(3)、若 ，求 的度数.23. 如图
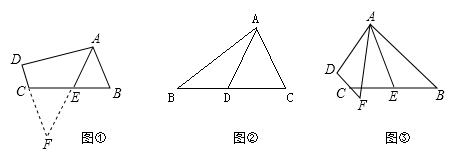(1)、如图①，在四边形ABCD中，AB∥CD，点E是BC的中点，若AE是∠BAD的平分线，试判断AB，AD，DC之间的等量关系。解决此问题可以用如下方法：延长AE交DC的延长线于点F，易证△AEB≌△FEC得到AB=FC，从而把AB，AD，DC转化在一个三角形中即可判断。
AB，AD，DC之间的等量关系；
(2)、同题探究；①如图②，AD是△ABC的中线，AB=6，AC=4，求AD的范围：
②如图③，在四边形ABCD中，AB∥CD，AF与DC的延长线交于点F，点E是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，并证明你的结论。
24. 阅读下列材料，然后解决问题：和、差、倍、分等问题中有着广泛的应用，截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段，或将某条线段延长，使之与某特定线段相等，再利用全等三角形的性质等有关知识来解决数学问题.
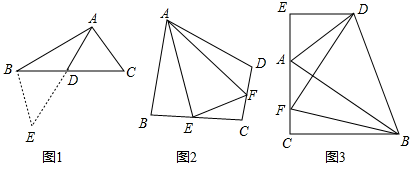(1)、如图1，在△ABC中，若AB=12，AC=8，求BC边上的中线AD的取值范围.解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE，把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线AD的取值范围是；
(2)、问题解决：如图2，在四边形ABCD中，AB=AD，∠ABC+∠ADC=180°，E、F分别是边BC，边CD上的两点，且∠EAF= ∠BAD，求证：BE+DF=EF.
(3)、问题拓展：如图3，在△ABC中，∠ACB=90°，∠CAB=60°，点D是△ABC外角平分线上一点，DE⊥AC交CA延长线于点E，F是AC上一点，且DF=DB.求证：AC-AE= AF.