初中数学浙教版2020-2021学年八年级上学期期中模拟试卷（1）
试卷更新日期：2020-10-18 类型：期中考试
一、单选题
-
1. 下列常用手机APP的图标中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 以下列各组长度的线段为边，能构成三角形的是 （ ）A、7，3，4 B、5，6，12 C、3，4，5 D、1，2，33. 若x＞y，则下列式子中错误的是（ ）A、x－3＞y－3 B、 ＞ C、x＋3＞y＋3 D、－3x＞－3y4. 如图，小丽画了一个三角形，不小心被墨水污染了，只剩下一个角（锐角）. 小丽画的三角形可能是（ ）
A、锐角三角形 B、直角三角形 C、钝角三角形 D、以上都有可能5. 下列所叙述的图形中，全等的两个三角形是（ ）A、含有45°角的两个直角三角形 B、腰相等的两个等腰三角形 C、边长相等的两个等边三角形 D、一个钝角对应相等的两个等腰三角形6. 下列命题正确的是（ ）A、如果两个角相等那么它们是对顶角 B、如果a=b，那么|a|=|b| C、面积相等的两个三角形全等 D、 如果
，那么a=b
7. 同学们都玩过跷跷板的游戏，如图是一个跷跷板的示意图，立柱OC与地面垂直，OA＝OB.当跷跷板的一头A着地时，∠AOA′=50°，则当跷跷板的另一头B着地时，∠COB′等于（ ）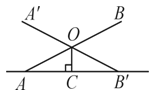
A、25° B、50° C、65° D、130°8. 一副透明的三角板，如图叠放，直角三角板的斜边AB、CE相交于点D，则∠BDC的度数为（ ）
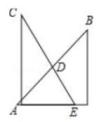A、60° B、45° C、75° D、90°9. 如图，BD是 的边AC上的中线，AE是 的边BD上的中线，BF是 的边AE上的中线，若 的面积是32，则 的面积是（ ）
A、8 B、9 C、18 D、1210. 如图，对角线AC将正方形ABCD分成两个等腰三角形，点E，F将对角线AC三等分，且AC=15，点P在正方形的边上，则满足PE+PF=5 的点P的个数是（ ）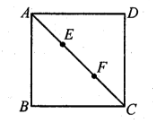
A、0 B、4 C、8 D、16二、填空题
-
11. 设三角形的三个内角分别为α、β、γ，且 ， ，则β的最大值与最小值的和是 ．12. 如图，数轴上所表示的不等式组的解集是 ．
13. 如图，已知BD是△ABC的中线，AB=5，BC=3，△ABD和△BCD的周长的差是.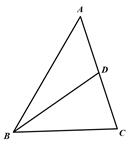
14. 如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠BAC交BC于点D，DE⊥AB于点E，若△BDE的周长是5 cm，则AB的长为.
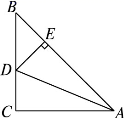15. 如图，在△ABC中，∠C=90°，BC=8cm，AC=6cm，点E是BC的中点，动点P从A点出发，先以每秒2cm的速度沿A→C运动，然后以1cm/s的速度沿C→B运动．若设点P运动的时间是t秒，那么当t= ， △APE的面积等于6．
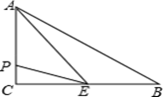16. 在△ABC中，边AB、AC的垂直平分线分别交边BC于点D、E，若∠DAE=40°，则∠BAC的度数为.
三、解答题
-
17. 解下列不等式，并把解集在数轴上表示出来(1)、2－5x≥8－2x(2)、18. 如图，已知△ABC，
(1)、求作点P，使点P到B、C两点的距离相等，且点P到∠BAC两边的距离也相等（尺规作图，保留作图痕迹，不写作法）.(2)、在（1）中，连接PB、PC，若∠BAC=40°，求∠BPC的度数.19. 如图，在四边形ABCD中，AD∥BC，E为CD的中点，连结AE，BE，延长AE交BC的延长线于点F。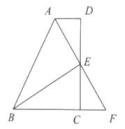
(1)、求证：△DAE≌△CFE；(2)、若BE⊥AF，求证：AB=BC+AD。20. 台风是一种自然灾害，它以台风中心为圆心，在周围数十千米范围内形气旋风暴，有极强的破坏力，此时某台风中心在海域B处，在沿海城市A的正南方向240千米，其中心风力为12级，每远离台风中心25千米，台风就会减弱一级，如图所示，该台风中心正以20千米/时的速度沿BC方向移动.已知AD⊥BC且AD= AB，且台风中心的风力不变，若城市所受风力达到或超过4级，则称受台风影响.试问：
(1)、A城市是否会受到台风影响？请说明理由.(2)、若会受到台风影响，那么台风影响该城市的持续时间有多长？(3)、该城市受到台风影响的最大风力为几级？21. 已知，DA，DB，DC是从点D出发的三条线段，且DA=DB=DC。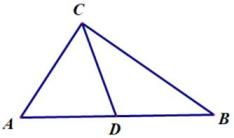
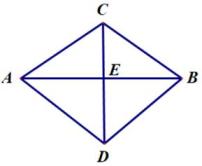(1)、如图①，若点D在线段AB上，连接AC，BC，试判断△ABC的形状，并说明理由。(2)、如图②，连接AC，BC，AB，且AB与CD相交于点E，若AC=BC，AB=16，DC=10，求CE和AC的长。22. 如图，在△ABC中，AB＝AC，∠B＝40°，点D在线段AB上运动（D不与B、C重合），连接AD，作∠ADE＝40°，DE交线段AC于点E．
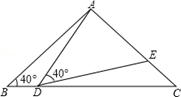(1)、若∠BDA＝115°，则∠BAD＝°，∠DEC＝°；(2)、若DC＝AB，求证：△ABD≌△DCE；(3)、在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数；若不可以，请说明理由．23. 如图，已知 中， ， ， ， 、 是 边上的两个动点，其中点 从点 开始沿 方向运动，且速度为每秒 ，点 从点 开始沿 方向运动，且速度为每秒 ，它们同时出发，设出发的时间为 秒．
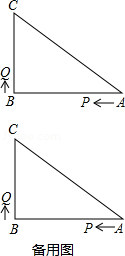(1)、出发2秒后，求 的长；(2)、从出发几秒钟后， 第一次能形成等腰三角形？(3)、当点 在边 上运动时，求能使 成为等腰三角形的运动时间．24. 如图，已知等边△ABC的边长为8，点P是AB边上的一个动点（与点A、B不重合），直线l是经过点P的一条直线，把△ABC沿直线l折叠，点B的对应点是点B’.
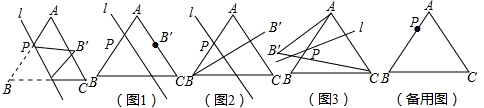(1)、如图1，当PB=4时，若点B’恰好在AC边上，则AB’的长度为；(2)、如图2，当PB=5时，若直线l//AC，则BB’的长度为；(3)、如图3，点P在AB边上运动过程中，若直线l始终垂直于AC，△ACB’的面积是否变化？若变化，说明理由；若不变化，求出面积；(4)、当PB=6时，在直线l变化过程中，求△ACB’面积的最大值.