吉林省长春市汽开区2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-10-16 类型：期末考试

进入出卷网下载

一、单选题

1. 已知x＝1是关于x的一元二次方程x²+mx﹣1＝0的一个根，则m的值是（）

A、0 B、1 C、2 D、﹣2

查看试题解析
2. 二次函数y＝﹣（x﹣1）²+2有（）

A、最大值1 B、最大值2 C、最小值1 D、最小值2

查看试题解析
3. 有5张完全相同的卡片，正面分别写有1，2，3，4，5这5个数字，现把卡片背面朝上，从中随机抽取一张卡片，其数字是奇数的概率为（）

A、 $\frac{2}{5}$ B、 $\frac{1}{2}$ C、 $\frac{3}{5}$ D、 $\frac{3}{4}$

查看试题解析
4. 已知点A（﹣2，y₁）、B（1，y₂）在二次函数y＝x²+2x+2的图象上，y₁与y₂的大小关系为（）

A、y₁＞y₂ B、y₁＝y₂ C、y₁＜y₂ D、y₁≤y₂

查看试题解析
5. 如图，四边形ABCD内接于⊙O ，若∠BCD＝110°，则∠BOD的度数为（）

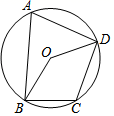A、35° B、70° C、110° D、140°

查看试题解析
6. 我国古代数学著作中记载了一个问题：“今有邑方不知大小，各开中门，出北门四十步有木，出西门八百一十步见木，问：邑方几何？”其大意是：一座正方形城池，西、北边正中各开一道门，从北门往正北方向走40步后刚好有一树木，若从西门往正西方向走810步后正好看到树木，则正方形城池的边长为（）步

A、360 B、270. C、180 D、90

查看试题解析
7. 已知二次函数 $y = a x^{2} + b x + c$ ( $a > 0$ )图象的对称轴是直线x=1，与x轴一个交点 $A (3, 0)$ ，则与 $x$ 轴的另一个交点坐标是（）

A、 $(0, - \frac{1}{2})$ B、 $(- \frac{1}{2}, 0)$ C、 $(0, - 1)$ D、 $(- 1, 0)$

查看试题解析
8. 如图，在每个小正方形的边长均为1的5×5的网格中，选取7个格点（小正方形的顶点），若以点A为圆心，r为半径画圆，选取的格点中除点A外恰好有3个点在圆内，则r的取值范围是（）

A、3＜r＜ $\sqrt{10}$ B、 $\sqrt{2}$ ＜r＜ $\sqrt{5}$ C、 $\sqrt{10}$ ＜r＜ $\sqrt{13}$ D、 $\sqrt{5}$ ＜r＜3

查看试题解析

二、填空题

9. 若关于x的方程x²﹣8x+m＝0有两个相等的实数根，则m＝．

查看试题解析
10. 将二次函数y＝x²﹣4x+7化为y＝（x﹣h）²+k的形式，结果为y＝．

查看试题解析
11. 如图，在平面直角坐标系中，点M的坐标为（ $\sqrt{5}$ ，2），则cosα的值为．

查看试题解析
12. 如图，点A、B、C、D、E、F均在⊙O上．若∠ADF＝20°，∠FEC＝35°，则∠ABC的大小为度．

查看试题解析
13. 小明分别以正六边形ABCDEF的顶点B、D、F为圆心，以BA长为半径作圆弧，设计出如图所示的图案．若AB＝1，则该图案外围轮廓的周长为．

查看试题解析
14. 一抛物线形拱桥如图所示，当拱顶离水面2m时，水面宽4m ．当水面下降1m时，水面的宽为m ．

查看试题解析

三、解答题

15. 解方程：x²﹣2x﹣6＝0．

查看试题解析
16. 在不透明的袋子中有2个红球和1个黑球，这些球除颜色外都相同，小明从中随机摸出一个球后放回并搅匀，小华再从中随机摸出一个球，用画树状图（或列表）的方法，求两人摸出相同颜色的球的概率．

查看试题解析
17. 图①、图②都是4×4的正方形网格，每个小正方形的顶点称为格点，已知△ABC的顶点均在格点上．

(1)、在图①中，以格点为顶点，画出△ADC ，使△ADC与△ABC全等，且点D与点B不重合．

(2)、在图②中，以格点为顶点，画出△AFC ，使△AFC与△ABC相似，且相似比不是1．（画出一个即可）

查看试题解析
18. 求图象为下列抛物线的二次函数的表达式；

(1)、抛物线y＝ax²+bx+2经过点（﹣2，6）、（2，2）．

(2)、抛物线的顶点坐标为（3，﹣5），且抛物线经过点（0，1）．

查看试题解析
19. 如图，AB是⊙O的直径，点C、D均在⊙O上，∠ACD＝30°，弦AD＝4cm ．

(1)、求⊙O的直径．

(2)、求 $\overset{⌢}{A D}$ 的长．

查看试题解析
20. 如表是小菲填写的实践活动报告的部分内容．

题目

测量铁塔顶端到地面的高度

测量目标

示意图

相关数据

CE＝25米，CD＝10米，∠FDG＝44°

求铁塔的高度FE ．（结果精确到1米）

（参考数据：sin44°＝0.69，cos44°＝0.72，tan44°＝0.97）

查看试题解析
21. 如图，AB是⊙O的弦，OP⊥OA交AB于点P，过点B的直线交OP的延长线于点C，且CP=CB．

(1)、求证：BC是⊙O的切线；

(2)、若⊙O的半径为 $\sqrt{5}$ ，OP=1，求BC的长．

查看试题解析
22. 如图

(1)、某学校“智慧方园”数学社团遇到这样一个题目：
如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO= $3 \sqrt{3}$ ，BO：CO=1：3，求AB的长．
经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．
请回答：∠ADB=°，AB= ．

(2)、请参考以上解决思路，解决问题：
如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO= $3 \sqrt{3}$ ，∠ABC=∠ACB=75°，BO：OD=1：3，求DC的长．

查看试题解析
23. 如图，射线AN上有一点B ， AB＝5，tan∠MAN＝ $\frac{4}{3}$ ，点C从点A出发以每秒3个单位长度的速度沿射线AN运动，过点C作CD⊥AN交射线AM于点D ，在射线CD上取点F ，使得CF＝CB ，连结AF ．设点C的运动时间是t（秒）（t＞0）．

(1)、当点C在点B右侧时，求AD、DF的长．（用含t的代数式表示）

(2)、连结BD ，设△BCD的面积为S平方单位，求S与t之间的函数关系式．

(3)、当△AFD是轴对称图形时，直接写出t的值．

查看试题解析
24. 在平面直角坐标系中，抛物线y＝﹣（x﹣m）²+4（m＞0）的顶点为A ，与直线x＝ $\frac{m}{2}$ 相交于点B ，点A关于直线x＝ $\frac{m}{2}$ 的对称点为C ．

(1)、若抛物线y＝﹣（x﹣m）²+4（m＞0）经过原点，求m的值．

(2)、点C的坐标为．用含m的代数式表示点B到直线AC的距离为．

(3)、将y＝﹣（x﹣m）²+4（m＞0，且x≥ $\frac{m}{2}$ ）的函数图象记为图象G ，图象G关于直线x＝ $\frac{m}{2}$ 的对称图象记为图象H ．图象G与图象H组合成的图象记为图象M ．
①当图象M与x轴恰好有三个交点时，求m的值．

②当△ABC为等腰直角三角形时，直接写出图象M所对应的函数值小于0时，自变量x的取值范围．

查看试题解析