吉林省延边州敦化市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-16 类型:期末考试
一、单选题
-
1. 抛物线 的顶点坐标为( )A、 B、 C、 D、2. 下列函数是 关于 的反比例函数的是( )A、 B、 C、 D、3. 下列品牌的运动鞋标志中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图, 是 的直径,点 、 、 在 上.若 ,则 的度数为( )
4. 如图, 是 的直径,点 、 、 在 上.若 ,则 的度数为( ) A、105° B、110° C、115° D、120°5. 如图,在 中, ,且DE分别交AB,AC于点D,E,若 ,则△ 和△ 的面积之比等于( )
A、105° B、110° C、115° D、120°5. 如图,在 中, ,且DE分别交AB,AC于点D,E,若 ,则△ 和△ 的面积之比等于( )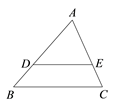 A、 B、 C、 D、6. 获2019年度诺贝尔化学奖的“锂电池”创造了一个更清洁的世界.我国新能源发展迅猛,某种特型锂电池2016年销售量为8万个,到2018年销售量为97万个.设年均增长率为x,可列方程为( )A、8(1+x)2=97 B、97(1﹣x)2=8 C、8(1+2x)=97 D、8(1+x2)=97
A、 B、 C、 D、6. 获2019年度诺贝尔化学奖的“锂电池”创造了一个更清洁的世界.我国新能源发展迅猛,某种特型锂电池2016年销售量为8万个,到2018年销售量为97万个.设年均增长率为x,可列方程为( )A、8(1+x)2=97 B、97(1﹣x)2=8 C、8(1+2x)=97 D、8(1+x2)=97二、填空题
-
7. 方程(x﹣1)2=4的解为 .8. 抛物线 与 轴交点坐标为.9. 如图,在平面直角坐标系中, 和 是以坐标原点 为位似中心的位似图形,且点B(3,1), ,(6,2),若点 (5,6),则点 的坐标为 .
 10. 若双曲线 的图象在第二、四象限内,则 的取值范围是 .11. 在一个不透明的塑料袋中装有红色白色球共 个.除颜色外其他都相同,小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在 左右,则口袋中红色球可能有个.12. 为测量学校旗杆的高度,小明的测量方法如下:如图,将直角三角形硬纸板DEF的斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上.测得DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米.按此方法,请计算旗杆的高度为米.
10. 若双曲线 的图象在第二、四象限内,则 的取值范围是 .11. 在一个不透明的塑料袋中装有红色白色球共 个.除颜色外其他都相同,小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在 左右,则口袋中红色球可能有个.12. 为测量学校旗杆的高度,小明的测量方法如下:如图,将直角三角形硬纸板DEF的斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上.测得DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米.按此方法,请计算旗杆的高度为米.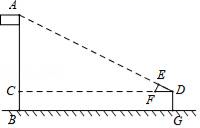 13. 如图,将正方形 绕点 逆时针旋转 至正方形 ,边 交 于点 ,若正方形 的边长为 ,则 的长为 .
13. 如图,将正方形 绕点 逆时针旋转 至正方形 ,边 交 于点 ,若正方形 的边长为 ,则 的长为 . 14. 如图,抛物线 交 轴于点 ,交 轴于点 ,在 轴上方的抛物线上有两点 ,它们关于 轴对称,点 在 轴左侧. 于点 , 于点 ,四边形 与四边形 的面积分别为6和10,则 与 的面积之和为 .
14. 如图,抛物线 交 轴于点 ,交 轴于点 ,在 轴上方的抛物线上有两点 ,它们关于 轴对称,点 在 轴左侧. 于点 , 于点 ,四边形 与四边形 的面积分别为6和10,则 与 的面积之和为 .
三、解答题
-
15. 解方程:3x(x﹣1)=2﹣2x.16. 如图,一块直角三角板的直角顶点 放在正方形 的边 上,并且使一条直角边经过点 .另一条直角边与 交于点 .求证: .
 17. 已知双曲线 经过点B(2,1).(1)、求双曲线的解析式;(2)、若点 与点 都在双曲线 上,且 ,直接写出 、 的大小关系.18. 甲、乙、丙、丁4位同学进行一次乒乓球单打比赛,要从中选2名同学打第一场比赛.(1)、已确定甲同学打第一场比赛,再从其余3名同学中随机选取1名,恰好选中乙同学的概率是;(2)、随机选取2名同学,求其中有乙同学的概率.19. 如图,在平面直角坐标系中, 三个顶点的坐标分别为A(2,3)、B(1,1)、C(5,1).
17. 已知双曲线 经过点B(2,1).(1)、求双曲线的解析式;(2)、若点 与点 都在双曲线 上,且 ,直接写出 、 的大小关系.18. 甲、乙、丙、丁4位同学进行一次乒乓球单打比赛,要从中选2名同学打第一场比赛.(1)、已确定甲同学打第一场比赛,再从其余3名同学中随机选取1名,恰好选中乙同学的概率是;(2)、随机选取2名同学,求其中有乙同学的概率.19. 如图,在平面直角坐标系中, 三个顶点的坐标分别为A(2,3)、B(1,1)、C(5,1). (1)、把 平移后,其中点 移到点 ,面出平移后得到的 ;(2)、把 绕点 按逆时针方向旋转 ,画出旋转后得到的 ,并求出旋转过程中点 经过的路径长(结果保留根号和 ).20. 已知抛物线 经过A(0,2)、B(4,0)、C(5,-3)三点,当 时,其图象如图所示.
(1)、把 平移后,其中点 移到点 ,面出平移后得到的 ;(2)、把 绕点 按逆时针方向旋转 ,画出旋转后得到的 ,并求出旋转过程中点 经过的路径长(结果保留根号和 ).20. 已知抛物线 经过A(0,2)、B(4,0)、C(5,-3)三点,当 时,其图象如图所示. (1)、求该抛物线的解析式,并写出该抛物线的顶点坐标;(2)、求该抛物线与 轴的另一个交点的坐标.21. 如图,在四边形 中, , .已知A(-2,0)、B(6,0)、D(0,3)反比例函数 的图象经过点 .
(1)、求该抛物线的解析式,并写出该抛物线的顶点坐标;(2)、求该抛物线与 轴的另一个交点的坐标.21. 如图,在四边形 中, , .已知A(-2,0)、B(6,0)、D(0,3)反比例函数 的图象经过点 . (1)、求点 的坐标和反比例函数 的解析式;(2)、将四边形 沿 轴向上平移2个单位长度得到四边形 ,问点 是否落在(1)中的反比例函数的图象上?22. 如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)、求点 的坐标和反比例函数 的解析式;(2)、将四边形 沿 轴向上平移2个单位长度得到四边形 ,问点 是否落在(1)中的反比例函数的图象上?22. 如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
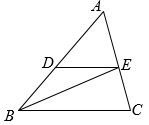 (1)、求证:AE•BC=BD•AC;(2)、如果 =3, =2,DE=6,求BC的长.23. 如图,点 是等边 中 边的延长线上的一点,且 .以 为直径作 ,分别交 、 于点 、 .
(1)、求证:AE•BC=BD•AC;(2)、如果 =3, =2,DE=6,求BC的长.23. 如图,点 是等边 中 边的延长线上的一点,且 .以 为直径作 ,分别交 、 于点 、 . (1)、求证: 是 的切线;(2)、连接 ,交 于点 ,若 ,求线段 、 与 围成的阴影部分的面积(结果保留根号和 ).24. 一次函数 与反比例函数 的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
(1)、求证: 是 的切线;(2)、连接 ,交 于点 ,若 ,求线段 、 与 围成的阴影部分的面积(结果保留根号和 ).24. 一次函数 与反比例函数 的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D. (1)、求一次函数与反比例函数的表达式;(2)、过点B作BC⊥y轴,垂足为C,连接AC交x轴于点E,求△AED的面积S.25. 如图,在 中, , , .动点 从点 出发,沿线段 向终点 以 / 的速度运动,同时动点 从点 出发,沿折线 以 / 的速度向终点 运动,当有一点到达终点时,另一点也停止运动,以 、 为邻边作设▱ 与 重叠部分图形的面积为 点 运动的时间为 .
(1)、求一次函数与反比例函数的表达式;(2)、过点B作BC⊥y轴,垂足为C,连接AC交x轴于点E,求△AED的面积S.25. 如图,在 中, , , .动点 从点 出发,沿线段 向终点 以 / 的速度运动,同时动点 从点 出发,沿折线 以 / 的速度向终点 运动,当有一点到达终点时,另一点也停止运动,以 、 为邻边作设▱ 与 重叠部分图形的面积为 点 运动的时间为 . (1)、当点 在 边上时,求 的长(用含 的代数式表示);(2)、当点 落在线段 上时,求 的值;(3)、求 与 之间的函数关系式 ,并写出自变量 的取值范围.26. 若二次函数 的图象的顶点在 的图象上,则称 为 的伴随函数,如 是 的伴随函数.(1)、若函数 是 的伴随函数,求 的值;(2)、已知函数 是 的伴随函数.
(1)、当点 在 边上时,求 的长(用含 的代数式表示);(2)、当点 落在线段 上时,求 的值;(3)、求 与 之间的函数关系式 ,并写出自变量 的取值范围.26. 若二次函数 的图象的顶点在 的图象上,则称 为 的伴随函数,如 是 的伴随函数.(1)、若函数 是 的伴随函数,求 的值;(2)、已知函数 是 的伴随函数.①当点(2,-2)在二次函数 的图象上时,求二次函数的解析式;
②已知矩形 , 为原点,点 在 轴正半轴上,点 在 轴正半轴上,点 (6,2),当二次函数 的图象与矩形 有三个交点时,求此二次函数的顶点坐标.