吉林省四平市铁西区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-16 类型:期末考试
一、单选题
-
1. 下列手机软件图标中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如果△ABC∽△DEF,相似比为2:1,且△DEF的面积为4,那么△ABC的面积为( )A、1 B、4 C、8 D、163. 如图,正六边形 内接于 ,连接 .则 的度数是( )
2. 如果△ABC∽△DEF,相似比为2:1,且△DEF的面积为4,那么△ABC的面积为( )A、1 B、4 C、8 D、163. 如图,正六边形 内接于 ,连接 .则 的度数是( )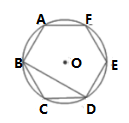 A、15° B、20° C、30° D、45°4. 如图,AB是⊙O的直径,∠AOC=130°,则∠D等于()
A、15° B、20° C、30° D、45°4. 如图,AB是⊙O的直径,∠AOC=130°,则∠D等于() A、25° B、35° C、50° D、65°5. 如图, 是等腰直角三角形,且 , 轴,点 在函数 的图象上,若 ,则 的值为( )
A、25° B、35° C、50° D、65°5. 如图, 是等腰直角三角形,且 , 轴,点 在函数 的图象上,若 ,则 的值为( )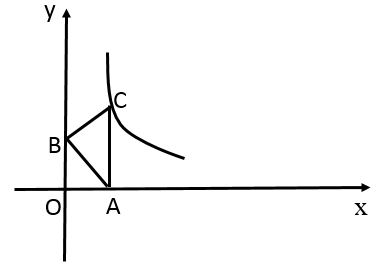 A、2 B、1 C、 D、6. 如图,抛物线 与 轴交于点 ,对称轴为 ,则下列结论中正确的是( )
A、2 B、1 C、 D、6. 如图,抛物线 与 轴交于点 ,对称轴为 ,则下列结论中正确的是( ) A、 B、当 时, 随 的增大而增大 C、 D、 是一元二次方程 的一个根
A、 B、当 时, 随 的增大而增大 C、 D、 是一元二次方程 的一个根二、填空题
-
7. 小强同学从0,1,2,3这四个数中任选一个数,满足不等式 的概率是 .8. 抛物线 的对称轴为 .9. 将抛物线 向左平移2个单位,再向上平移1个单位后,得到的抛物线的解析式为 .10. 为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为 的大视力表制作一个测试距离为 的小视力表.如图,如果大视力表中“ ”的高度是 ,那么小视力表中相应“ ”的高度是 .
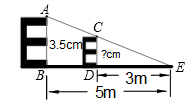 11. 如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合连接CD , 则∠BDC的度数为度.
11. 如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合连接CD , 则∠BDC的度数为度.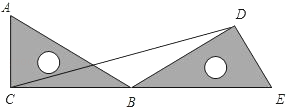 12. 已知抛物线 经过 和 两点,则 的值为 .13. 如图,在半径为 的圆形铁片上切下一块高为 的弓形铁片,则弓形弦 的长为cm.
12. 已知抛物线 经过 和 两点,则 的值为 .13. 如图,在半径为 的圆形铁片上切下一块高为 的弓形铁片,则弓形弦 的长为cm.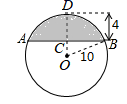 14. 如图所示,矩形纸片 中, ,把它分割成正方形纸片 和矩形纸片 后,分别裁出扇形 和半径最大的圆,恰好能作一个圆锥的侧面和底面,则 的长为.
14. 如图所示,矩形纸片 中, ,把它分割成正方形纸片 和矩形纸片 后,分别裁出扇形 和半径最大的圆,恰好能作一个圆锥的侧面和底面,则 的长为.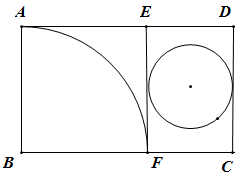
三、解答题
-
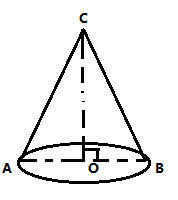
15. 小明同学用纸板制作了一个圆锥形漏斗模型,如图所示,它的底面半径 ,高 ,求这个圆锥形漏斗的侧面积.
 16. 如图,将△ABC绕点B旋转得到△DBE,且A,D,C三点在同一条直线上.求证:DB平分∠ADE.
16. 如图,将△ABC绕点B旋转得到△DBE,且A,D,C三点在同一条直线上.求证:DB平分∠ADE.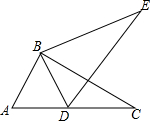 17. 在一个不透明的布袋中,有2个红球,1个白球,这些球除颜色外都相同(1)、搅匀后从中任意摸出1个球,摸到红球的概率是;(2)、搅匀后先从中任意摸出1个球(不放回),再从余下的球中任意摸出1个球.求两次都摸到红球的概率.(用树状图或表格列出所有等可能出现的结果)18. 如图, 中,顶点 的坐标是 , 轴, 交 轴于点 ,顶点 的纵坐标是-4, 的面积是24.反比例函数 的图象经过点 和 ,求反比例函数的表达式.
17. 在一个不透明的布袋中,有2个红球,1个白球,这些球除颜色外都相同(1)、搅匀后从中任意摸出1个球,摸到红球的概率是;(2)、搅匀后先从中任意摸出1个球(不放回),再从余下的球中任意摸出1个球.求两次都摸到红球的概率.(用树状图或表格列出所有等可能出现的结果)18. 如图, 中,顶点 的坐标是 , 轴, 交 轴于点 ,顶点 的纵坐标是-4, 的面积是24.反比例函数 的图象经过点 和 ,求反比例函数的表达式.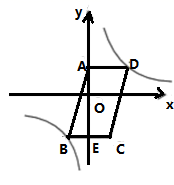 19. 如图, 的顶点坐标分别为 , , .
19. 如图, 的顶点坐标分别为 , , . (1)、画出 关于点 的中心对称图形 ;(2)、画出 绕原点 逆时针旋转 的 ,直接写出点 的坐标为;(3)、若 内一点 绕原点 逆时针旋转 的对应点为 ,则 的坐标为 . (用含 , 的式子表示)20. 如图, 中, , , 为 内部一点, .求证: .
(1)、画出 关于点 的中心对称图形 ;(2)、画出 绕原点 逆时针旋转 的 ,直接写出点 的坐标为;(3)、若 内一点 绕原点 逆时针旋转 的对应点为 ,则 的坐标为 . (用含 , 的式子表示)20. 如图, 中, , , 为 内部一点, .求证: .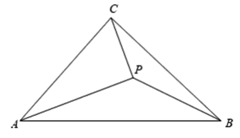 21. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象分别相交于第一、三象限内的 , 两点,与 轴交于点 .
21. 如图,在平面直角坐标系中,一次函数 的图象与反比例函数 的图象分别相交于第一、三象限内的 , 两点,与 轴交于点 .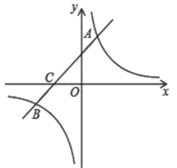 (1)、求该反比例函数和一次函数的解析式;(2)、在 轴上找到一点 使 最大,请直接写出此时点 的坐标.22. 抛物线 上部分点的横坐标 ,纵坐标 的对应值如下表:
(1)、求该反比例函数和一次函数的解析式;(2)、在 轴上找到一点 使 最大,请直接写出此时点 的坐标.22. 抛物线 上部分点的横坐标 ,纵坐标 的对应值如下表:-3
-2
-1
0
1
0
_________
4
3
0
(1)、把表格填写完整;(2)、根据上表填空:①抛物线与 轴的交点坐标是和;
②在对称轴右侧, 随 增大而;
③当 时,则 的取值范围是;
(3)、请直接写出抛物线 的解析式.23. 如图, 内接于 ,直径 交 于点 ,延长 至点 ,使 ,且 ,连接 并延长交过点 的切线于点 ,且满足 ,连接 .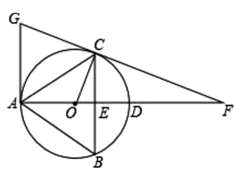 (1)、求证: ;(2)、求证: 是 的切线.24. 方方驾驶小汽车匀速地从 地行驶到 地,行驶里程为480千米,设小汽车的行驶时间为 (单位:小时),行驶速度为 (单位:千米/小时),且全程速度限定为不超过 千米/小时.(1)、求 关于 的函数表达式,并写出自变量 的取值范围;(2)、方方上午8点驾驶小汽车从 地出发;
(1)、求证: ;(2)、求证: 是 的切线.24. 方方驾驶小汽车匀速地从 地行驶到 地,行驶里程为480千米,设小汽车的行驶时间为 (单位:小时),行驶速度为 (单位:千米/小时),且全程速度限定为不超过 千米/小时.(1)、求 关于 的函数表达式,并写出自变量 的取值范围;(2)、方方上午8点驾驶小汽车从 地出发;①方方需在当天12点48分至14点(含12点48分和14点)间到达 地,求小汽车行驶速度 的范围;
②方方能否在当天11点30分前到达 地?说明理由.
25. 如图1是实验室中的一种摆动装置, 在地面上,支架 是底边为 的等腰直角三角形,摆动臂长 可绕点A旋转,摆动臂 可绕点D旋转, , . (1)、在旋转过程中:
(1)、在旋转过程中:①当 三点在同一直线上时,求 的长;
②当 三点在同一直角三角形的顶点时,求 的长.
(2)、若摆动臂 顺时针旋转 ,点 的位置由 外的点 转到其内的点 处,连结 ,如图2,此时 , ,求 的长.26. 如图,在平面直角坐标系中,已知抛物线 与 轴交于 , 两点,与 轴交于点 ,连接 . (1)、求抛物线的解析式;(2)、点 在抛物线的对称轴上,当 的周长最小时,点 的坐标为;(3)、点 是第四象限内抛物线上的动点,连接 和 .求 面积的最大值及此时点 的坐标;(4)、若点 是对称轴上的动点,在抛物线上是否存在点 ,使以点 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点 在抛物线的对称轴上,当 的周长最小时,点 的坐标为;(3)、点 是第四象限内抛物线上的动点,连接 和 .求 面积的最大值及此时点 的坐标;(4)、若点 是对称轴上的动点,在抛物线上是否存在点 ,使以点 、 、 、 为顶点的四边形是平行四边形?若存在,请直接写出点 的坐标;若不存在,请说明理由.