初中数学苏科版八年级上册4.3 实数同步练习

试卷更新日期：2020-10-16 类型：同步测试

进入出卷网下载

一、单选题

1. 在下列四个实数中，最小的数是（）

A、-2 B、 C、0 D、

查看试题解析
2. 下列说法正确的是

A、 $\sqrt{2}$ 是最小的无理数 B、 $\sqrt[3]{- 2}$ 的绝对值是 $\sqrt[3]{2}$ C、 $\sqrt{2}$ 的相反数是 $\sqrt{- 2}$ D、 $\sqrt[3]{2}$ 比 $\sqrt{2}$ 大

查看试题解析
3. 如图， $A B = A C$ ，则数轴上点C所表示的数为（）.

A、 $\sqrt{5} + 1$ B、 $\sqrt{5} - 1$ C、 $- \sqrt{5} + 1$ D、 $- \sqrt{5} - 1$

查看试题解析
4. 实数a ， b ， c ， d 在数轴上对应点的位置如图所示，则正确的结论是（）

A、a＞－4 B、bd＞0 C、b + c＞0 D、| a |＞|b|

查看试题解析
5. 按如图所示的程序计算，若开始输入的n值为 $\sqrt{2}$ ，则最后输出的结果是（）

A、14 B、16 C、8+5 $\sqrt{2}$ D、14+ $\sqrt{2}$

查看试题解析
6. 计算8的立方根与 $\sqrt{81}$ 的平方根之和是（　　）

A、5 B、11 C、5或﹣1 D、11或﹣7

查看试题解析
7. 比较两个实数 $\frac{\sqrt{5} - 1}{2}$ 与 $\frac{1}{2}$ 的大小，下列正确的是（）

A、 $\frac{\sqrt{5} - 1}{2} > \frac{1}{2}$ B、 $\frac{\sqrt{5} - 1}{2} < \frac{1}{2}$ C、 $\frac{\sqrt{5} - 1}{2} = \frac{1}{2}$ D、 $\frac{\sqrt{5} - 1}{2} 与 \frac{1}{2}$ 的大小不确定

查看试题解析
8. 在实数范围内定义运算“♀”，该运算同时满足下列条件：（1）x♀x=5，（x≠5）；（2）x♀（y♀z）=（x♀y）+z，则2015♀2017的值是（）

A、2 B、3 C、2015 D、2017

查看试题解析
9. 下列命题中：①有限小数是有理数；②无限小数都是无理数；③任意两个无理数的和还是无理数；④开方开不尽的数是无理数；⑤一个数的算术平方根一定是正数；⑥一个数的立方根一定比这个数小；⑦任意两个有理数之间都有有理数，任意两个无理数之间都有无理数.⑧有理数和数轴上的点一一对应；⑨不带根号的数一定是有理数；⑩负数没有立方根.其中正确的有（）

A、 $3$ 个 B、 $4$ 个 C、 $5$ 个 D、 $6$ 个

查看试题解析
10. 如图，半径为1的圆从表示1的点开始沿着数轴向左滚动一周，圆上的点A与表示1的点重合，滚动一周后到达点B，点B表示的数是（　　）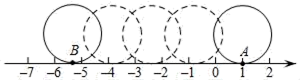

A、﹣2π B、1﹣2π C、﹣π D、1﹣π

查看试题解析

二、填空题

11. 比较大小： $\sqrt{8}$ 3．

查看试题解析
12. 下列实数：12，- $\frac{π}{3}$ ，|﹣1|， $\sqrt[3]{27}$ ，0.1010010001…， $\sqrt{37}$ ， ${(\sqrt{2})}^{0}$ 中，有理数有个.

查看试题解析
13. 如图所示的数轴上，点B与点C关于点A对称，A、B两点对应的实数是 $\sqrt{3}$ 和﹣1，则点C所对应的实数是．

查看试题解析
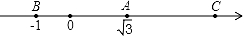14. 如图，△ABC的边BC在数轴上，AB⊥BC，且BC＝3，AB＝1，以C为圆心，AC长为半径画圆分别交数轴于点A′、点A″，那么数轴上点A′、点A″所表示的数分别是、.

查看试题解析
15. 如图所示，把边长为1的正方形放在数轴上，以数1表示的点为圆心，正方形的对角线长为半径作弧，交数轴于点A，则点A表示的数是．

查看试题解析
16. 在数轴上，点A表示实数 $\sqrt{7} - \sqrt{8}$ ,点B表示实数 $\sqrt{6} - \sqrt{7}$ ,那么A,B两点中离原点较远的点是.

查看试题解析
17. 对于任意不相等的两个实数a，b．定义运算※如下：a※b= $\frac{\sqrt{a + b}}{\sqrt{a - b}}$ ，如3※2= $\frac{\sqrt{3 + 2}}{\sqrt{3 - 2}}$ = $\sqrt{5}$ ，那么8※4= ．

查看试题解析
18. 设S₁=1+ $\frac{1}{1^{2}}$ + $\frac{1}{2^{2}}$ ，S₂=1+ $\frac{1}{2^{2}}$ + $\frac{1}{3^{2}}$ ，S₃=1+ $\frac{1}{3^{2}}$ + $\frac{1}{4^{2}}$ ，…，S_n=1+ $\frac{1}{n^{2}}$ + $\frac{1}{{(n + 1)}^{2}}$ ，设S= $\sqrt{S_{1}}$ + $\sqrt{S_{2}}$ +…+ $\sqrt{S_{n}}$ ，则S=（用含n的代数式表示，其中n为正整数）．

查看试题解析

三、解答题

19. 把下列各数填入相应的集合内
5 ， $\sqrt{14}$ ，6 ， $\sqrt{\frac{9}{17}}$ ， $\frac{3}{2}$ ， $\sqrt[3]{8}$ ，-π ，-0.13

⑴有理数集合｛                                     ｝

⑵无理数集合｛                                     ｝

⑶正实数集合｛                                     ｝

⑷负实数集合｛                                     ｝

查看试题解析
20.
在数轴上点A表示的数是 $\sqrt{5}$ ．
（1）若把点A向左平移2个单位得到点为B，则点B表示的数是什么？
（2）点C和（1）中的点B所表示的数互为相反数，点C表示的数是什么？
（3）求出线段OA，OB，OC的长度之和．

查看试题解析
21. 设 $S_{1} = 1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}$ ， $S_{2} = 1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}$ ， $S_{3} = 1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}$ ，…， $S_{n} = 1 + \frac{1}{n^{2}} + \frac{1}{{(n + 1)}^{2}}$ ．若 $S = \sqrt{S_{1}} + \sqrt{S_{2}} + \dots + \sqrt{S_{n}}$ ，求S（用含n的代数式表示，其中n为正整数）．

查看试题解析
22. 如图，在数轴上有两个长方形ABCD和EFGH，这两个长方形的宽都是2 $\sqrt{2}$ 个单位长度，长方形ABCD的长AD是4 $\sqrt{2}$ 个单位长度，长方形EFGH的长EH是8 $\sqrt{2}$ 个单位长度，点E在数轴上表示的数是5 $\sqrt{2}$ ，且E、D两点之间的距离为12 $\sqrt{2}$ 。

(1)、点H在数轴上表示的数是点，点A在数轴上表示的数是。

(2)、若线段AD的中点为M，线段EH上有一点N，EN= $\frac{1}{4}$ EH，M以每秒4个单位长度的速度向右匀速运动，N以每秒3个单位长度的速度向左运动，设运动的时间为x秒，问当x为多少时，原点O恰为线段MN的三等分点？

(3)、若线段AD的中点为M，线段EH上有一点N，EN= $\frac{1}{4}$ EH，长方形ABCD以每秒4个单位长度的速度向右匀速运动，长方形EFGH保持不动，设运动时间为t秒，是否存在一个t的值，使以M、N、F三点为顶点的三角形是直角三角形？若存在，求t的值；不存在，请说明理由。

查看试题解析

初中数学苏科版八年级上册4.3 实数 同步练习

一、单选题

二、填空题

三、解答题

初中数学苏科版八年级上册4.3 实数同步练习