广东省肇庆市端州区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-16 类型:期末考试
一、单选题
-
1. ﹣2的绝对值是( )A、2 B、 C、 D、-22. 据有关部门统计,2019年“五一小长假”期间,广东各大景点共接待游客约14400000人次,将数14400000用科学记数法表示为( )A、 B、 C、 D、3. 下图中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
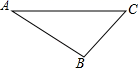
D、 4. 平面直角坐标系内与点P(﹣2,3)关于原点对称的点的坐标是( )A、(3,﹣2) B、(2,3) C、(2,﹣3) D、(﹣3,﹣3)5. 如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
4. 平面直角坐标系内与点P(﹣2,3)关于原点对称的点的坐标是( )A、(3,﹣2) B、(2,3) C、(2,﹣3) D、(﹣3,﹣3)5. 如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )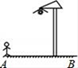 A、逐渐变短 B、先变短后变长 C、先变长后变短 D、逐渐变长6. 要得到抛物线y=2(x﹣4)2+1,可以将抛物线y=2x2( )A、向左平移4个单位长度,再向上平移1个单位长度 B、向左平移4个单位长度,再向下平移1个单位长度 C、向右平移4个单位长度,再向上平移1个单位长度 D、向右平移4个单位长度,再向下平移1个单位长度7. 现有四张分别标有数字﹣2,﹣1,1,3的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张卡片,记下数字后放回,洗匀,再随机抽取一张卡片,则第一次抽取的卡片上的数字大于第二次抽取的卡片上的数字的概率是( )A、 B、 C、 D、8. 菱形ABCD的一条对角线长为6,边AB的长是方程x2﹣7x+12=0的一个根,则菱形ABCD的周长为( )A、16 B、12 C、16或12 D、249. 如图,在平面直角坐标系中,四边形 为菱形, , , ,则对角线交点 的坐标为( )
A、逐渐变短 B、先变短后变长 C、先变长后变短 D、逐渐变长6. 要得到抛物线y=2(x﹣4)2+1,可以将抛物线y=2x2( )A、向左平移4个单位长度,再向上平移1个单位长度 B、向左平移4个单位长度,再向下平移1个单位长度 C、向右平移4个单位长度,再向上平移1个单位长度 D、向右平移4个单位长度,再向下平移1个单位长度7. 现有四张分别标有数字﹣2,﹣1,1,3的卡片,它们除数字外完全相同,把卡片背面朝上洗匀,从中随机抽取一张卡片,记下数字后放回,洗匀,再随机抽取一张卡片,则第一次抽取的卡片上的数字大于第二次抽取的卡片上的数字的概率是( )A、 B、 C、 D、8. 菱形ABCD的一条对角线长为6,边AB的长是方程x2﹣7x+12=0的一个根,则菱形ABCD的周长为( )A、16 B、12 C、16或12 D、249. 如图,在平面直角坐标系中,四边形 为菱形, , , ,则对角线交点 的坐标为( )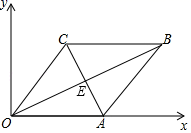 A、 B、 C、 D、10. 如图,在矩形 中, , ,过对角线交点 作 交 于点 ,交 于点 ,则 的长是( )
A、 B、 C、 D、10. 如图,在矩形 中, , ,过对角线交点 作 交 于点 ,交 于点 ,则 的长是( ) A、1 B、 C、2 D、
A、1 B、 C、2 D、二、填空题
-
11. 当时, 在实数范围内有意义.12. 分解因式:4x3﹣9x= .13. 抛物线y=﹣3(x﹣1)2+2的开口向 , 对称轴为 , 顶点坐标为 .14. 方程x(x﹣2)﹣x+2=0的正根为 .15. 方程x2﹣4x﹣6=0的两根和等于 , 两根积等于 .16. 正六边形的中心角为;当它的半径为1时,边心距为 .17. 圆锥的侧面展开图是一个形,设圆锥的母线长为3,底面圆的半径为2,则这个圆锥的全面积为 .
三、解答题
-
18. 先化简,再求值: ,其中a=3,b=﹣2.19. 如图,利用尺规,在△ABC的边AC下方作∠CAE=∠ACB,在射线AE上截取AD=BC,连接CD,并证明:CD=AB.(尺规作图要求保留作图痕迹,不写作法)
 20. 受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素,我市某汽车零部件生产企业的利润逐年提高,据统计,2014年利润为2亿元,2016年利润为2.88亿元.(1)、求该企业从2014年到2016年利润的年平均增长率;(2)、若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润能否超过3.4亿元?21. 如图, 已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F. 试说明:
20. 受益于国家支持新能源汽车发展和“一带一路”发展战略等多重利好因素,我市某汽车零部件生产企业的利润逐年提高,据统计,2014年利润为2亿元,2016年利润为2.88亿元.(1)、求该企业从2014年到2016年利润的年平均增长率;(2)、若2017年保持前两年利润的年平均增长率不变,该企业2017年的利润能否超过3.4亿元?21. 如图, 已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F. 试说明: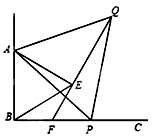 (1)、△ABP≌△AEQ;(2)、EF=BF22. 某区规定学生每天户外体育活动时间不少于1小时,为了解学生参加户外体育活动的情况,对部分学生每天参加户外体育活动的时间进行了随机抽样调查,并将调查结果绘制成如图的统计图表(不完整).请根据图表中的信息,解答下列问题:
(1)、△ABP≌△AEQ;(2)、EF=BF22. 某区规定学生每天户外体育活动时间不少于1小时,为了解学生参加户外体育活动的情况,对部分学生每天参加户外体育活动的时间进行了随机抽样调查,并将调查结果绘制成如图的统计图表(不完整).请根据图表中的信息,解答下列问题: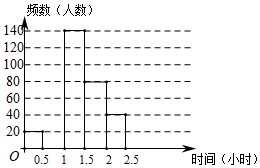 (1)、表中的a= , 将频数分布直方图补全;(2)、该区8000名学生中,每天户外体育活动的时间不足1小时的学生大约有多少名?(3)、若从参加户外体育活动时间最长的3名男生和1名女生中随机抽取两名,请用画树状图或列表法求恰好抽到1名男生和1名女生的概率.
(1)、表中的a= , 将频数分布直方图补全;(2)、该区8000名学生中,每天户外体育活动的时间不足1小时的学生大约有多少名?(3)、若从参加户外体育活动时间最长的3名男生和1名女生中随机抽取两名,请用画树状图或列表法求恰好抽到1名男生和1名女生的概率.组别
时间(小时)
频数(人数)
频率
A
0≤t<0.5
20
0.05
B
0.5≤t<1
a
0.3
C
l≤t<1.5
140
0.35
D
1.5≤t<2
80
0.2
E
2≤t<2.5
40
0.1
23. 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.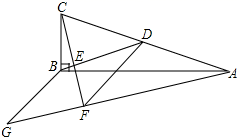 (1)、求证:四边形BDFG为菱形;(2)、若AG=13,CF=6,求四边形BDFG的周长.24. 如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC、OD交于点E.
(1)、求证:四边形BDFG为菱形;(2)、若AG=13,CF=6,求四边形BDFG的周长.24. 如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC、OD交于点E.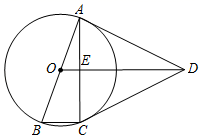 (1)、求证:OD∥BC;(2)、若AC=2BC,求证:DA与⊙O相切.25. 如图,已知抛物线 与y轴相交于点A(0,3),与x正半轴相交于点B,对称轴是直线x=1.
(1)、求证:OD∥BC;(2)、若AC=2BC,求证:DA与⊙O相切.25. 如图,已知抛物线 与y轴相交于点A(0,3),与x正半轴相交于点B,对称轴是直线x=1.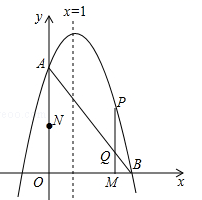 (1)、求此抛物线的解析式以及点B的坐标.(2)、动点M从点O出发,以每秒2个单位长度的速度沿x轴正方向运动,同时动点N从点O出发,以每秒3个单位长度的速度沿y轴正方向运动,当N点到达A点时,M、N同时停止运动.过动点M作x轴的垂线交线段AB于点Q,交抛物线于点P,设运动的时间为t秒.
(1)、求此抛物线的解析式以及点B的坐标.(2)、动点M从点O出发,以每秒2个单位长度的速度沿x轴正方向运动,同时动点N从点O出发,以每秒3个单位长度的速度沿y轴正方向运动,当N点到达A点时,M、N同时停止运动.过动点M作x轴的垂线交线段AB于点Q,交抛物线于点P,设运动的时间为t秒.①当t为何值时,四边形OMPN为矩形.
②当t>0时,△BOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.