广东省湛江市雷州市2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-10-16 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
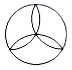 B、
B、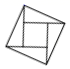 C、
C、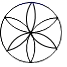 D、
D、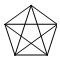 2. 用配方法解一元二次方程 时,方程变形正确的是( )A、 B、 C、 D、3. 抛物线y=(x-3)2+4的顶点坐标是( )A、(-1,2) B、(-1,-2) C、(1,-2) D、(3,4)4. 一元二次方程x2﹣4x+5=0的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 如图,⊙O是△ABC的外接圆,连接OC、OB,∠BOC=100°,则∠A的度数为( )
2. 用配方法解一元二次方程 时,方程变形正确的是( )A、 B、 C、 D、3. 抛物线y=(x-3)2+4的顶点坐标是( )A、(-1,2) B、(-1,-2) C、(1,-2) D、(3,4)4. 一元二次方程x2﹣4x+5=0的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 如图,⊙O是△ABC的外接圆,连接OC、OB,∠BOC=100°,则∠A的度数为( )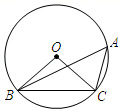 A、30° B、40° C、50° D、60°6. 抛物线y=x2﹣4x+1与y轴交点的坐标是( )A、(0,1) B、(1,O) C、(0,﹣3) D、(0,2)7. 下列成语所描述的事件是必然发生的是( )A、水中捞月 B、拔苗助长 C、守株待兔 D、瓮中捉鳖8. 抛物线y=x2先向右平移1个单位,再向上平移3个单位,得到新的抛物线解析式是( )A、y=(x+1)2+3 B、y=(x+1)2﹣3 C、y=(x﹣1)2﹣3 D、y=(x﹣1)2+39. 如图, 是 的弦,半径 于点 且 则 的长为( ).
A、30° B、40° C、50° D、60°6. 抛物线y=x2﹣4x+1与y轴交点的坐标是( )A、(0,1) B、(1,O) C、(0,﹣3) D、(0,2)7. 下列成语所描述的事件是必然发生的是( )A、水中捞月 B、拔苗助长 C、守株待兔 D、瓮中捉鳖8. 抛物线y=x2先向右平移1个单位,再向上平移3个单位,得到新的抛物线解析式是( )A、y=(x+1)2+3 B、y=(x+1)2﹣3 C、y=(x﹣1)2﹣3 D、y=(x﹣1)2+39. 如图, 是 的弦,半径 于点 且 则 的长为( ).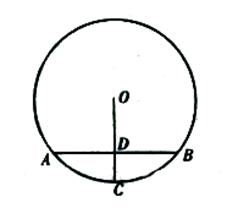 A、 B、 C、 D、10. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( )A、x(x+1)=1035 B、x(x-1)=1035 C、 x(x+1)=1035 D、 x(x-1)=1035
A、 B、 C、 D、10. 某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为( )A、x(x+1)=1035 B、x(x-1)=1035 C、 x(x+1)=1035 D、 x(x-1)=1035二、填空题
-
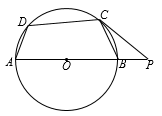
11. 方程x2=1的解是 .12. 点P(2,﹣1)关于原点的对称点坐标为(﹣2,m),则m= .13. 已知二次函数y=(x﹣2)2﹣3,当x<2时,y随x的增大而(填“增大”或“减小”).14. 如果关于x的方程x2﹣5x+k=0没有实数根,那么k的值为15. 扇形的弧长为10πcm , 面积为120πcm2 , 则扇形的半径为cm .16. 抛物线y=x2+2x﹣3的对称轴是 .17. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,过点C作⊙O的切线交AB的延长线于点P,若∠P=40°,则∠ADC=°.
三、解答题
-
18. 解方程:x2﹣2x﹣3=0;19. 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2).(正方形网格中每个小正方形的边长是一个单位长度),
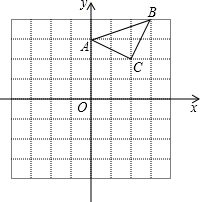 (1)、在正方形网格中画出△ABC绕点O顺时针旋转90°得到△A1B1C1 .(2)、求出线段OA旋转过程中所扫过的面积(结果保留π).20. 已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.(1)、如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;(3)、如果△ABC是等边三角形,试求这个一元二次方程的根.21. 据媒体报道,我国2009年公民出境旅游总人数约5000万人次,2011年公民出境旅游总人数约7200万人次,若2010年、2011年公民出境旅游总人数逐年递增,请解答下列问题:(1)、求这两年我国公民出境旅游总人数的年平均增长率;(2)、如果2012年仍保持相同的年平均增长率,请你预测2012年我国公民出境旅游总人数约多少万人次.22. 一个不透明的口袋中装有4个分别标有数1,2,3,4的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为x,小颖在剩下的3个球中随机摸出一个小球记下数为y,这样确定了点P的坐标(x,y).(1)、小红摸出标有数3的小球的概率是 .(2)、请你用列表法或画树状图法表示出由x,y确定的点P(x,y)所有可能的结果.(3)、求点P(x,y)在函数y=﹣x+5图象上的概率.23. 已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)、在正方形网格中画出△ABC绕点O顺时针旋转90°得到△A1B1C1 .(2)、求出线段OA旋转过程中所扫过的面积(结果保留π).20. 已知关于x的一元二次方程(a+c)x2+2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.(1)、如果x=﹣1是方程的根,试判断△ABC的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;(3)、如果△ABC是等边三角形,试求这个一元二次方程的根.21. 据媒体报道,我国2009年公民出境旅游总人数约5000万人次,2011年公民出境旅游总人数约7200万人次,若2010年、2011年公民出境旅游总人数逐年递增,请解答下列问题:(1)、求这两年我国公民出境旅游总人数的年平均增长率;(2)、如果2012年仍保持相同的年平均增长率,请你预测2012年我国公民出境旅游总人数约多少万人次.22. 一个不透明的口袋中装有4个分别标有数1,2,3,4的小球,它们的形状、大小完全相同,小红先从口袋里随机摸出一个小球记下数为x,小颖在剩下的3个球中随机摸出一个小球记下数为y,这样确定了点P的坐标(x,y).(1)、小红摸出标有数3的小球的概率是 .(2)、请你用列表法或画树状图法表示出由x,y确定的点P(x,y)所有可能的结果.(3)、求点P(x,y)在函数y=﹣x+5图象上的概率.23. 已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.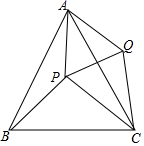 (1)、求证:△BAP≌△CAQ.(2)、若PA=3,PB=4,∠APB=150°,求PC的长度.24. 如图,AB是⊙O的直径,点C、D在⊙O上,且AD平分∠CAB,过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F,G为AB的下半圆弧的中点,DG交AB于H,连接DB、GB.
(1)、求证:△BAP≌△CAQ.(2)、若PA=3,PB=4,∠APB=150°,求PC的长度.24. 如图,AB是⊙O的直径,点C、D在⊙O上,且AD平分∠CAB,过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F,G为AB的下半圆弧的中点,DG交AB于H,连接DB、GB.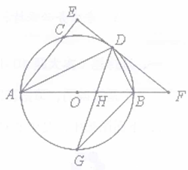 (1)、证明EF是⊙O的切线;(2)、求证:∠DGB=∠BDF:(3)、已知圆的半径R=5,BH=3,求GH的长.25. 已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,
(1)、证明EF是⊙O的切线;(2)、求证:∠DGB=∠BDF:(3)、已知圆的半径R=5,BH=3,求GH的长.25. 已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,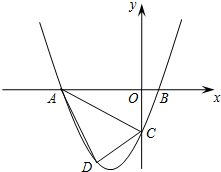 (1)、求抛物线的解析式;(2)、若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(1)、求抛物线的解析式;(2)、若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.