广东省汕头市龙湖区2019-2020学年九年级上学期数学期末试卷
试卷更新日期：2020-10-16 类型：期末考试
一、单选题
-
1. 下列方程中，是一元二次方程的是（ ）A、x+ ＝0 B、ax2+bx+c＝0 C、x2+1＝0 D、x﹣y﹣1＝02. 下列手机手势解锁图案中，是中心对称图形的是（ ）A、
B、
C、
D、
3. 用配方法解方程x2﹣2x﹣5=0时，原方程应变形为（ ）A、（x+1）2=6 B、（x+2）2=9 C、（x﹣1）2=6 D、（x﹣2）2=94. 事件①：射击运动员射击一次，命中靶心；事件②：购买一张彩票，没中奖，则（ ）A、事件①是必然事件，事件②是随机事件 B、事件①是随机事件，事件②是必然事件 C、事件①和②都是随机事件 D、事件①和②都是必然事件5. 抛物线y=(x+2)2-3的对称轴是（ ）A、直线 x=2 B、直线x=-2 C、直线x=-3 D、直线x=36. 关于反比例函数y＝﹣ 的图象，下列说法正确的是（ ）A、经过点(﹣1，﹣4) B、图象是轴对称图形，但不是中心对称图形 C、无论x取何值时，y随x的增大而增大 D、点( ，﹣8)在该函数的图象上7. 如图，AB是⊙O的直径，直线PA与⊙O相切于点A，PO交⊙O于点C，连接BC．若∠P＝40°，则∠ABC的度数为（ ）
A、20° B、25° C、40° D、50°8. 若关于x的方程kx2﹣2x﹣1＝0有实数根，则实数k的取值范围是（ ）A、k＞﹣1 B、k＜1且k≠0 C、k≥﹣1且k≠0 D、k≥﹣19. 如图，直线y=2x与双曲线 在第一象限的交点为A，过点A作AB⊥x轴于B，将△ABO绕点O旋转90°，得到△A′B′O，则点A′的坐标为（ ）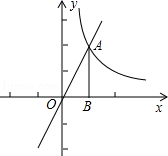
A、（1.0） B、（1.0）或（﹣1.0） C、（2.0）或（0，﹣2） D、（﹣2.1）或（2，﹣1）10. 如图，是二次函数y＝ax2+bx+c图象的一部分，其对称轴是x＝﹣1，且过点(﹣3，0)，下列说法：①abc＜0；②2a﹣b＝0；③若(﹣5，y1)，(3，y2)是抛物线上两点，则y1＝y2；④4a+2b+c＜0，其中说法正确的（ ）
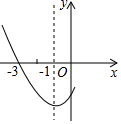A、①② B、①②③ C、①②④ D、②③④二、填空题
-
11. 点P(4，﹣6)关于原点对称的点的坐标是 ．12. 抛物线y＝﹣2x2+3x﹣7与y轴的交点坐标为 ．13. 已知正六边形的边长为10，那么它的外接圆的半径为 ．14. 白云航空公司有若干个飞机场，每两个飞机场之间都开辟一条航线，一共开辟了10条航线，则这个航空公司共有个飞机场．15. 如图，在平面直角坐标系中，直线l∥x轴，且直线l分别与反比例函数y= （x＞0）和y=﹣ （x＜0）的图象交于点P、Q，连结PO、QO，则△POQ的面积为 ．
16. 如图，在4×4的正方形网格中，若将△ABC绕着点A逆时针旋转得到△AB′C′，则 的长为 ．
17. 如图，Rt△ABC中，∠C=90°，∠ABC=30°，AC=2，△ABC绕点C顺时针旋转得△A1B1C，当A1落在AB边上时，连接B1B，取BB1的中点D，连接A1D，则A1D的长度是 ．
三、解答题
-
18. 解方程：x2﹣4x﹣12=0．19. 网购已经成为一种时尚，某网络购物平台“双十一”全天交易额逐年增长，2017年交易额为500亿元，2019年交易额为720亿元，求2017年至2019年“双十一”交易额的年平均增长率．20. 在校园文化艺术节中，九年级一班有1名男生和2名女生获得美术奖，另有1名男生和1名女生获得音乐奖．(1)、从获得美术奖和音乐奖的5名学生中选取1名参加颁奖大会，刚好是男生的概率是；(2)、分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会，用列表或树状图求刚好是一男生一女生的概率．21. 如图，破残的圆形轮片上，弦 的垂直平分线交 于点 ，交弦 于点 .已知 cm ， c m.
(1)、求作此残片所在的圆；(不写作法，保留作图痕迹)(2)、求（1）中所作圆的半径.22. 如图，将等边△ABC绕点C顺时针旋转90°得到△EFC，∠ACE的平分线CD交EF于点D，连接AD、AF．
(1)、求∠CFA度数；(2)、求证：AD∥BC．23. 如图，一次函数y=﹣x+4的图象与反比例函数y= （k为常数，且k≠0）的图象交于A（1，a），B（3，b）两点．
(1)、求反比例函数的表达式；(2)、在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标；(3)、求△PAB的面积．24. 如图，AB、CD为⊙O的直径，弦AE∥CD ， 连接BE交CD于点F ， 过点E作直线EP与CD的延长线交于点P ， 使∠PED＝∠C ．
(1)、求证：PE是⊙O的切线；(2)、求证：DE平分∠BEP；(3)、若⊙O的半径为10，CF＝2EF ， 求BE的长．25. 如图，抛物线y＝﹣x2+bx+c与x轴相交于A、B两点，与y轴相交于点C ， 且点B与点C的坐标分别为B(3，0)，C(0，3)，点M是抛物线的顶点．
(1)、求二次函数的关系式；(2)、点P为线段MB上一个动点，过点P作PD⊥x轴于点D ． 若OD＝m ， △PCD的面积为S ，①求S与m的函数关系式，写出自变量m的取值范围．
②当S取得最值时，求点P的坐标；
(3)、在MB上是否存在点P ， 使△PCD为直角三角形？如果存在，请直接写出点P的坐标；如果不存在，请说明理由．