广东省汕头市潮南区司马浦镇2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-10-16 类型：期末考试

进入出卷网下载

一、单选题

1. 抛物线 $y = {(x - 1)}^{2} + 2$ 的顶点坐标是（）

A、（﹣1，2） B、（﹣1，﹣2） C、（1，﹣2） D、（1，2）

查看试题解析
2. 已知关于x的一元二次方程x²+3x﹣2＝0，下列说法正确的是（）

A、方程有两个相等的实数根 B、方程有两个不相等的实数根 C、没有实数根 D、无法确定

查看试题解析
3. 下列图形中，是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，点B，C，D在⊙O上，若∠BCD＝130°，则∠BOD的度数是（）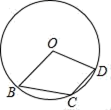

A、50° B、60° C、80° D、100°

查看试题解析
5. 如图，将△ABC绕点C顺时针旋转90°得到△EDC ．若点A ， D ， E在同一条直线上，∠ACB=20°，则∠ADC的度数是（）

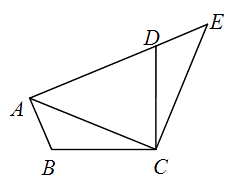A、55° B、60° C、65° D、70°

查看试题解析
6. 用配方法解方程 $x^{2} + 2 x - 3 = 0$ 时，可将方程变形为（）

A、 ${(x + 1)}^{2} = 2$ B、 ${(x - 1)}^{2} = 2$ C、 ${(x - 1)}^{2} = 4$ D、 ${(x + 1)}^{2} = 4$

查看试题解析
7. 如图，PA，PB切⊙O于点A，B，点C是⊙O上一点，且∠P＝36°，则∠ACB＝（）

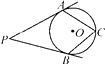A、54° B、72° C、108° D、144°

查看试题解析
8. 若将半径为6cm的半圆形纸片围成一个圆锥的侧面，则这个圆锥的底面圆半径是（）

A、1cm B、2cm C、3cm D、4cm

查看试题解析
9. 有n支球队参加篮球比赛，共比赛了15场，每两个队之间只比赛一场，则下列方程中正确的是（）

A、n(n﹣1)＝15 B、n(n+1)＝15 C、n(n﹣1)＝30 D、n(n+1)＝30

查看试题解析
10. 铅球运动员掷铅球的高度y(m)与水平距离x(m)之间的函数关系式为y＝－ $\frac{1}{12}$ x²＋ $\frac{2}{3}$ x＋ $\frac{5}{3}$ .则该运动员此次掷铅球的成绩是(　　)

A、6 m B、12 m C、8 m D、10 m

查看试题解析

二、填空题

11. 方程（x﹣3）（x+2）=0的根是．

查看试题解析
12. 如图，⊙O的直径AB垂直于弦CD，垂足为E.如果∠B＝60°，AC＝6，那么CD的长为.

查看试题解析
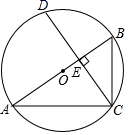13. 若关于 $x$ 的一元二次方程(m-1)x²-4x+1=0有两个不相等的实数根，则m的取值范围为．

查看试题解析
14. 若点P(2a+3b，﹣2)关于原点的对称点为Q(3，a﹣2b)，则(3a+b)²⁰²⁰＝.

查看试题解析
15. 在一个不透明的袋子中装有除颜色外完全相同的3个白球、若干红球，从中随机摸取1个球，摸到红球的概率是 $\frac{5}{8}$ ，则这个袋子中有红球个．

查看试题解析
16. 已知 $⊙ O$ 的半径为 $10 c m$ ， $A B$ ， $C D$ 是 $⊙ O$ 的两条弦， $A B / / C D$ ， $A B = 16 c m$ ， $C D = 12 c m$ ，则弦 $A B$ 和 $C D$ 之间的距离是 $c m$ ．

查看试题解析
17. 如图，将含有45°角的直角三角板ABC（∠C=90°）绕点A顺时针旋转30°得到△AB′C′，连接BB′，已知AC=2，则阴影部分面积为．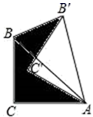

查看试题解析

三、解答题

18. 解方程： $x^{2} - 8 x + 1 = 0$ （配方法）

查看试题解析
19. 一个不透明的盒子中装有2枚黑色的棋子和1枚白色的棋子，每枚棋子除了颜色外其余均相同．从盒中随机摸出一枚棋子，记下颜色后放回并搅匀，再从盒子中随机摸出一枚棋子，记下颜色，用画树状图（或列表）的方法，求两次摸出的棋子颜色不同的概率．

查看试题解析
20. 如图，在 $Rt △ ABC$ 中， $∠ C = 90^{\circ}$ ， $∠ B = 30^{\circ}$ ．

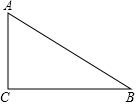(1)、用直尺和圆规作 $⊙ O$ ，使圆心O在BC边，且 $⊙ O$ 经过A，B两点上 $($ 不写作法，保留作图痕迹 $)$ ；

(2)、连接AO，求证：AO平分 $∠ CAB$ ．

查看试题解析
21. 已知关于x的方程（a﹣1）x²+2x+a﹣1＝0．

(1)、若该方程有一根为2，求a的值及方程的另一根；

(2)、当a为何值时，方程的根仅有唯一的值？求出此时a的值及方程的根．

查看试题解析
22. 如图，四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，且点E在线段AD上，若AF=4，∠F=60°．

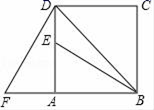(1)、指出旋转中心和旋转角度；

(2)、求DE的长度和∠EBD的度数．

查看试题解析
23. 为满足市场需求，某超市在五月初五“端午节”来临前夕，购进一种品牌粽子，每盒进价是40元，超市规定每盒售价不得少于45元．根据以往销售经验发现：当售价定为每盒45元时，每天可卖出700盒，每盒售价每提高1元，每天要少卖出20盒．

(1)、试求出每天的销售量y（盒）与每盒售价x（元）之间的函数关系式；

(2)、当每盒售价定为多少元时，每天销售的利润P（元）最大？最大利润是多少？

查看试题解析
24. 如图， $A B$ 是⊙ $O$ 的直径， $A P$ 是⊙ $O$ 的切线，点 $A$ 为切点， $B P$ 与⊙ $O$ 交于点 $C$ ，点 $D$ 是 $A P$ 的中点，连结 $C D$ ．

(1)、求证： $C D$ 是⊙ $O$ 的切线；

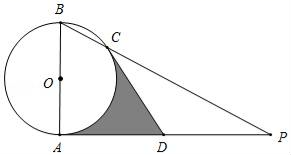(2)、若 $A B = 2$ ， $∠ P = 30^{0}$ ，求阴影部分的面积．

查看试题解析
25. 如图，已知直线AB经过点（0，4），与抛物线y= $\frac{1}{4}$ x²交于A，B两点，其中点A的横坐标是 $- 2$ .

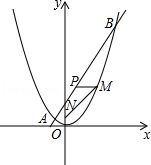(1)、求这条直线的函数关系式及点B的坐标.

(2)、在x轴上是否存在点C，使得△ABC是直角三角形？若存在，求出点C的坐标，若不存在请说明理由.

(3)、过线段AB上一点P，作PM∥x轴，交抛物线于点M，点M在第一象限，点N（0，1），当点M的横坐标为何值时，MN+3MP的长度最大？最大值是多少？

查看试题解析